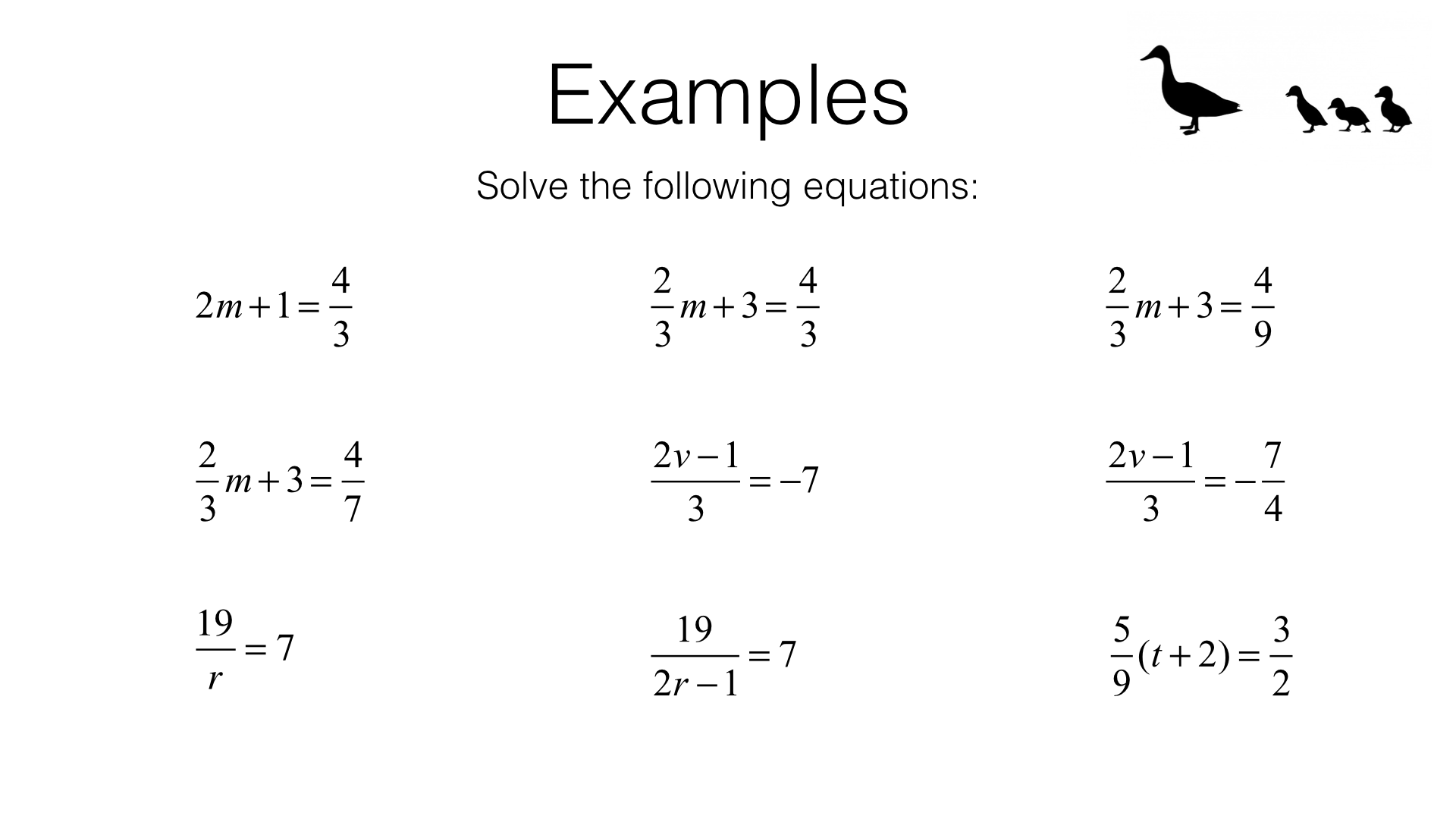This is the students’ version of the page. Log in above for the teachers’ version.

A starting point: solving an equation

We solve an equation by finding its solution. This applet generates equations in \(x\). This means that the \(x\) in these equations is variable—it can take any value. In the case of these equations, however, the equation is only true for one particular value of \(x\). This is the solution. We say that this satisfies the equation. When we substitute the solution into the equation, the value of the left hand side is equal to the value of the right hand side.

This applet represents each side of the equation using algebra tiles. The green \(x\) tiles are resizable. By dragging the slider, try to find can what \(x\) must be to make the two towers the same height. This value of \(x\) is the solution to the equation.

Skill isolation: Maintaining equality

Students should realise that equations can be seen like a balance. Whether seeing this as “doing the same thing to both sides” or a process of “breaking and repairing”, it is also important that students appreciate that it is mathematically valid to manipulate equations in many ways—and not just in ways that lead to simpler equations or even a solution. Of course, the skill is most often used in pursuit of a solution, but the skill is well worth practising in its own right.

This applet allows you to start with an equation, and perform certain steps that don’t necessarily lead to a solution but do let you practise manipulating both sides of an equation in a consistent manner. At difficulty levels 2 and 3, choose the “Show random steps” option to practise this.

To practise solving equations, choose the “Show only simplifying steps option” (visible in difficulty levels 2 and 3). Note that clicking this option repeatedly for a given equation will demonstrate that there may be different ways to solve it efficiently. For example, given \(2x+5=7\), the first step might be to subtract \(5\), add \(-5\), divide by \(2\), or multiply by \(\frac{1}{2}\). Following any of these first steps, it is possible to solve the equation in one further step.

Drag down the slider to reveal the result of each step. Click the “New equation” button to generate a new equation.

Part 1 – Solving simple linear equations in one unknown algebraically (easy)

Part 2 – Solving simple linear equations in one unknown algebraically (hard)

Interactive GeoGebra applet: Solving equations step-by-step

This applet generates equations at your chosen difficulty level. You can also type in your own expressions to create a custom equation. (Take care when typing your own expressions; you may end up with an equation that has no solutions.)

Then you can then go about solving the equation. You may like to decide what you could do to one side of the equation (e.g. add, subtract, multiply or divide by a quantity, which could be a constant or an expression involving \(x\)) to make that side of the equation simpler. If you only do this to one side of the equation, you break the equation, so you’ll need to do it to the other side to repair the equation. In other words, you need to do the same thing to both sides. Then simplify both sides where possible. Repeat the process until you have solved the equation.

This applet should help you see what effect each operation has on different types of expressions. With some practice, you should be able to identify accurate and efficient routes to the solutions of these equations.