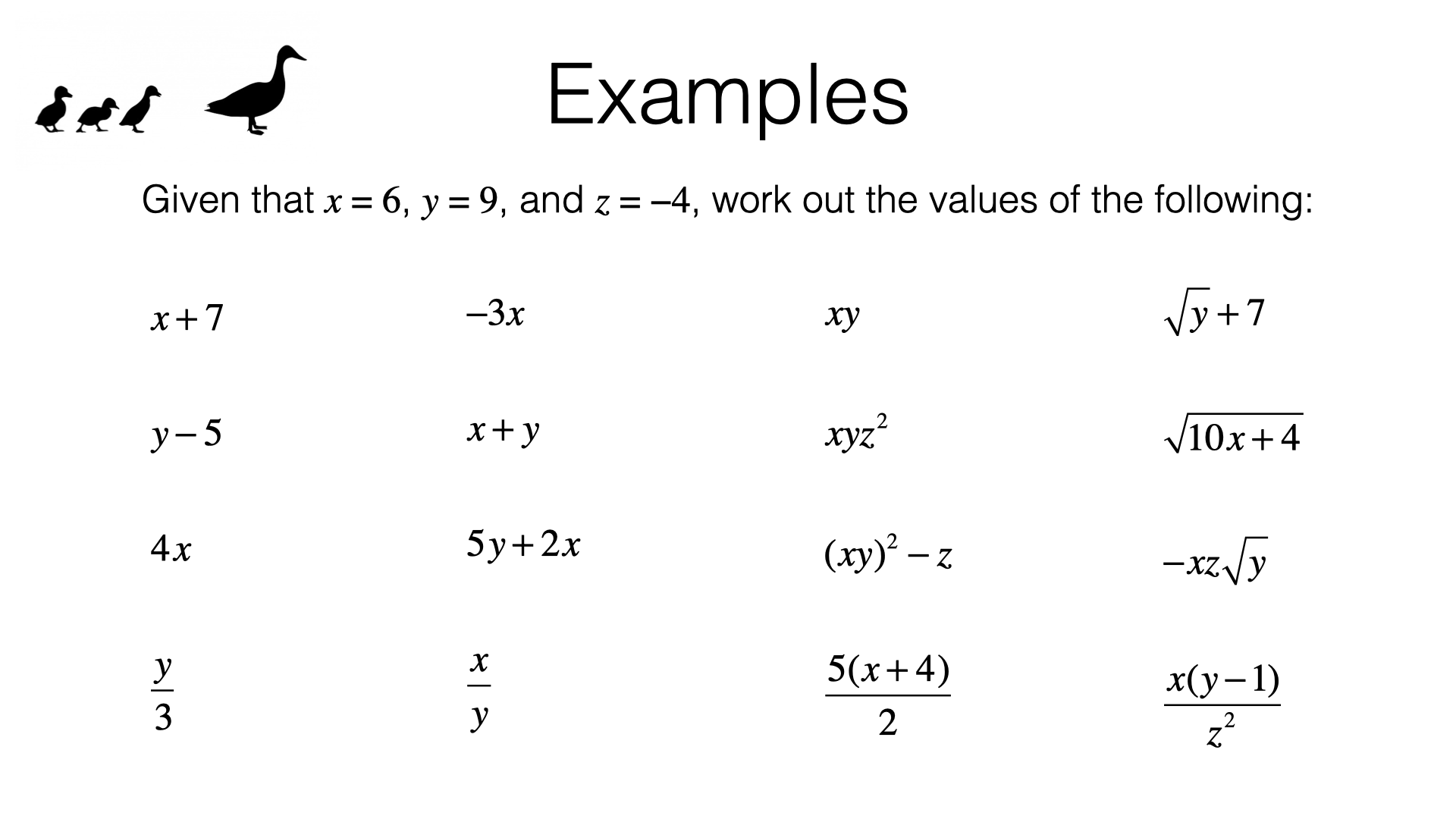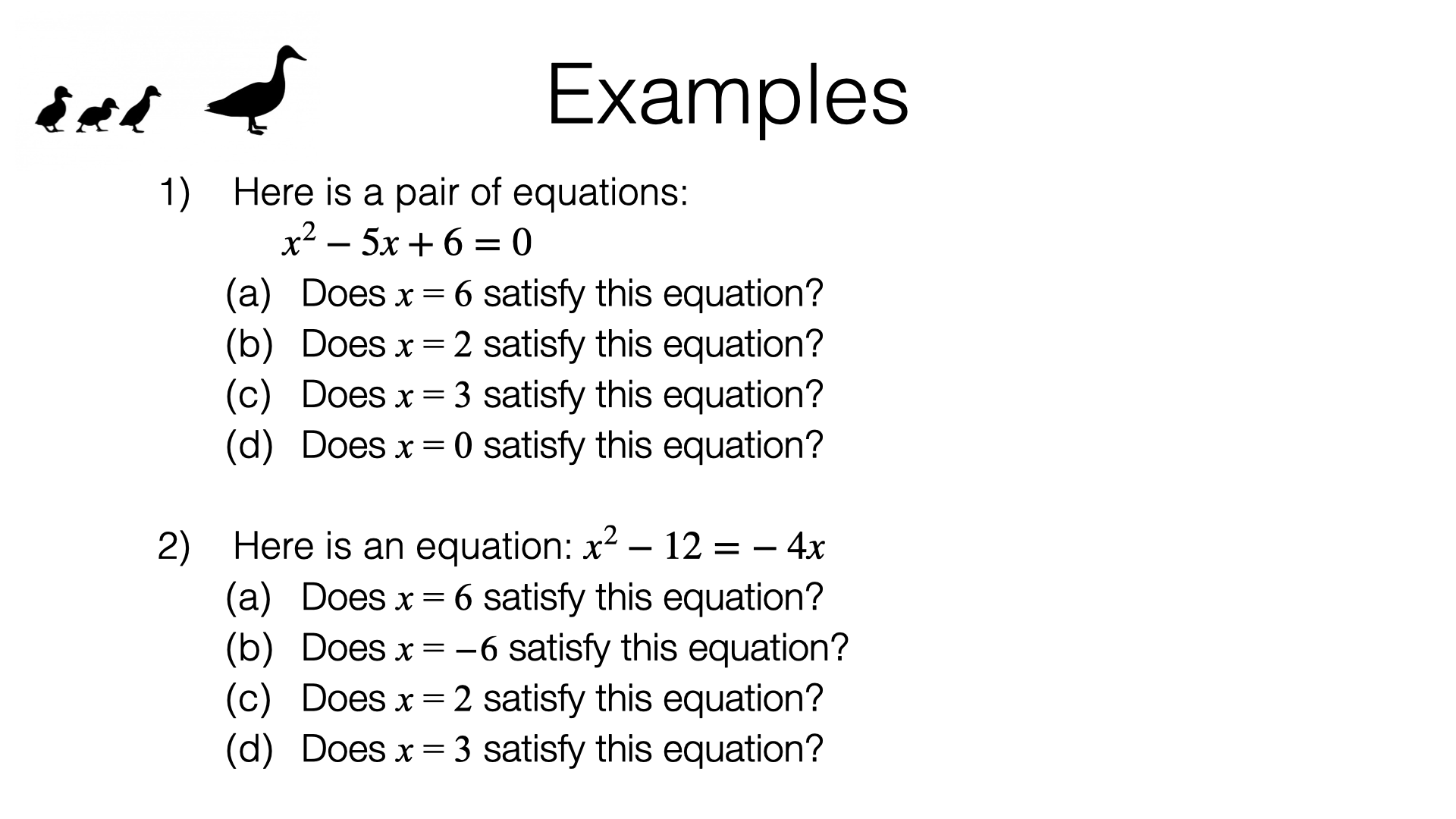This is the students’ version of the page. Log in above for the teachers’ version.
- A1a – Using and interpreting algebraic notation (essential)
- A3a – Understanding and using the concepts of expressions, equations, formulas, identities, inequalities, terms and factors (essential)
- N9b – Multiplying and dividing in standard form (helpful for Part 1 Exam-style question 5)
- A4b – Multiplying a single term over a bracket (required for Part 3 only)
- A4d – Multiplying two or more brackets (required for Part 3 only)
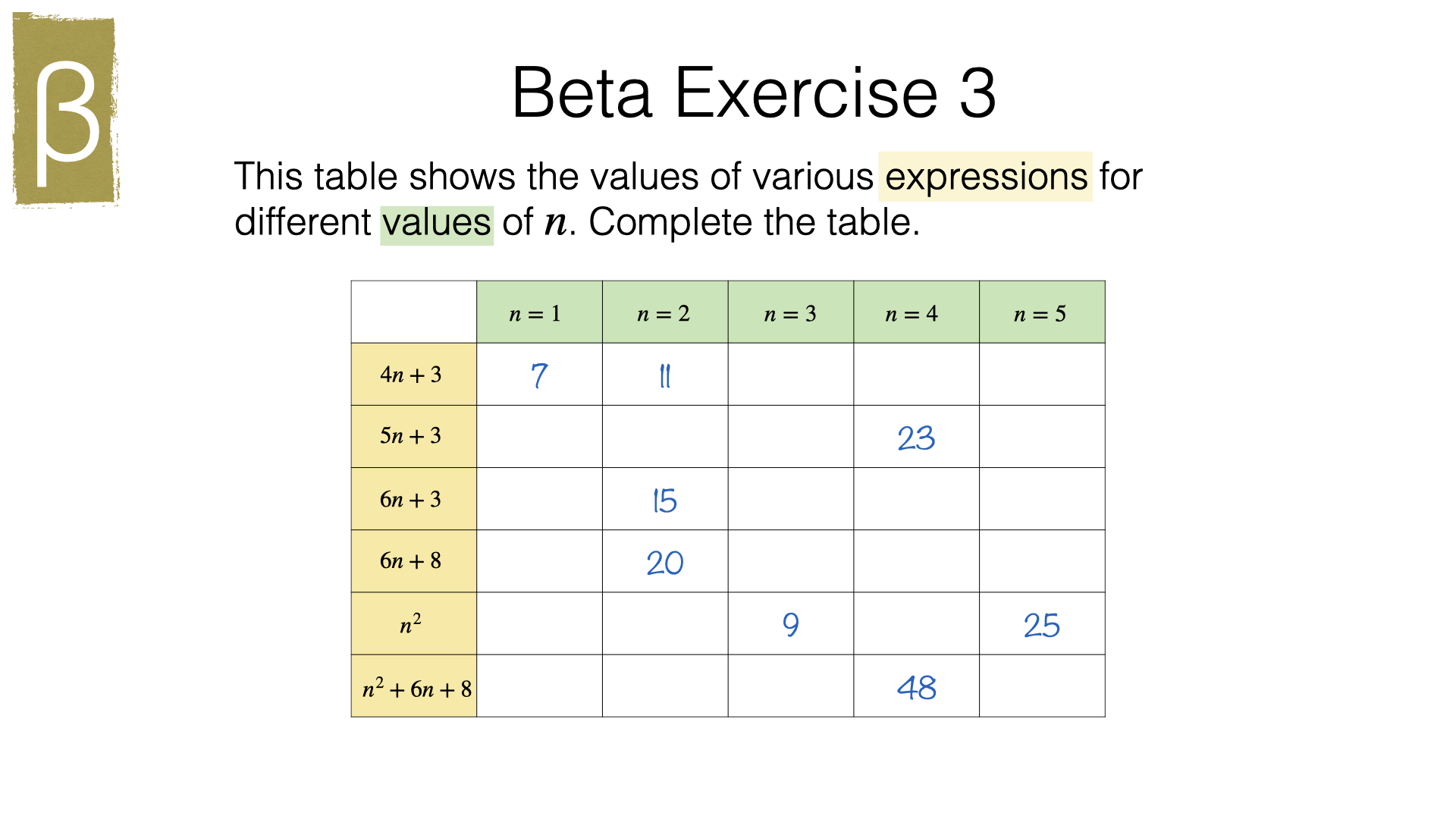
A starting point: substitution without numbers
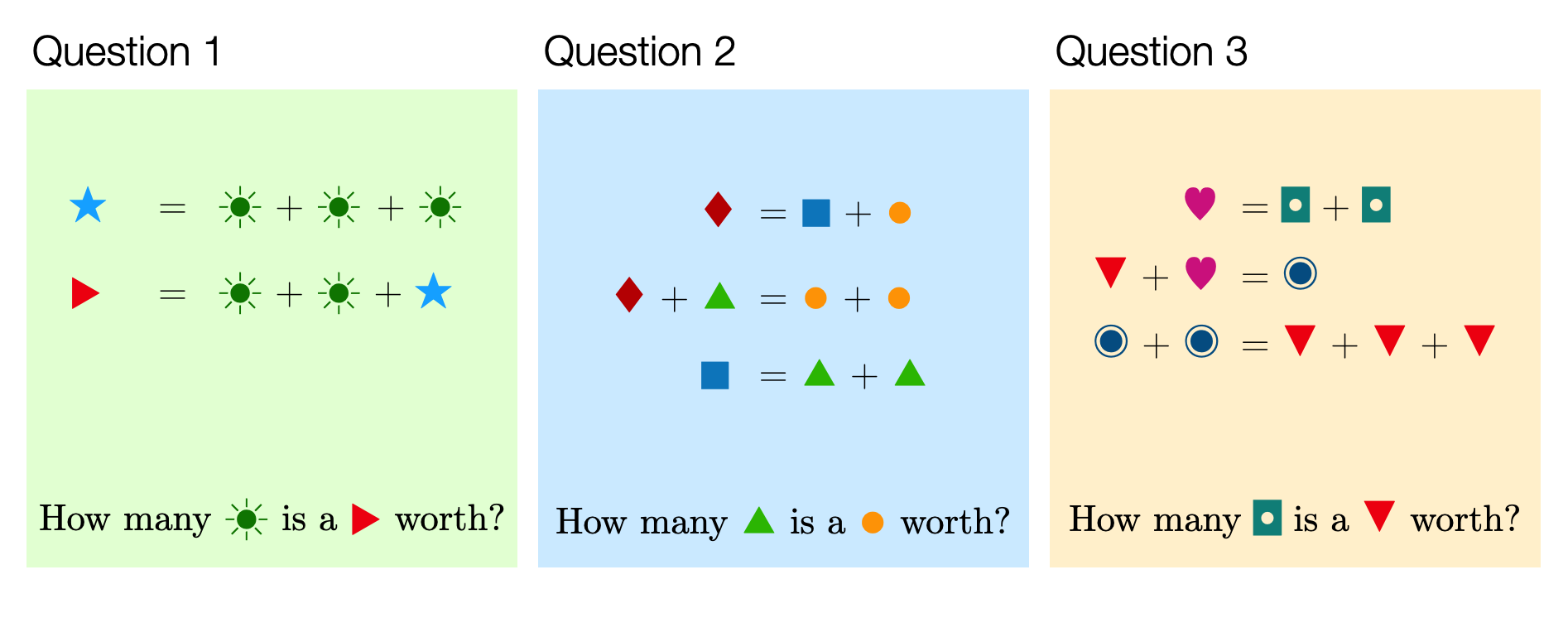
Part 1 – Substituting numerical values into expressions and formulas
Teachers: log in to access these.
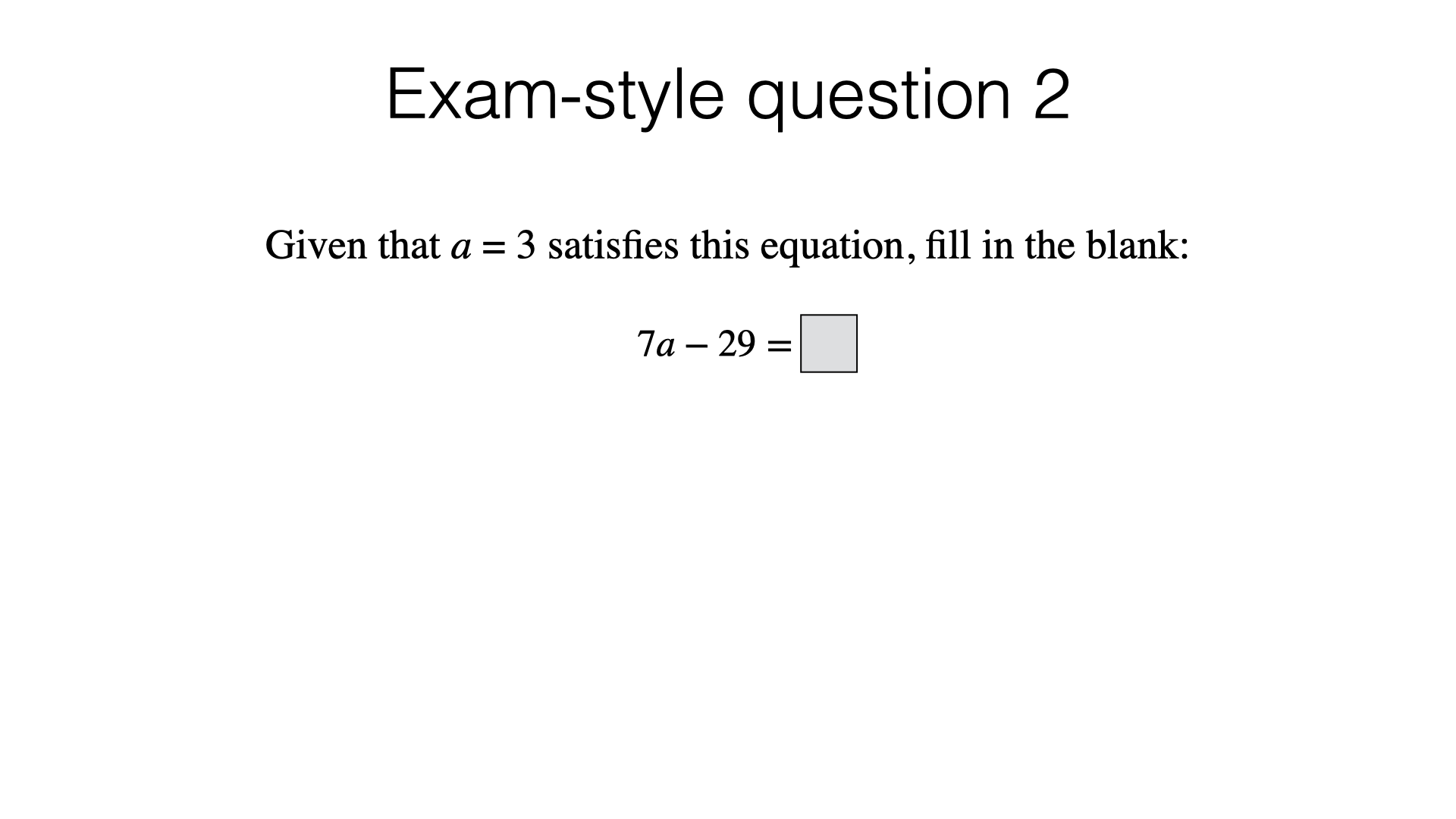
Part 2 – Substituting to check equations are satisfied
Teachers: log in to access these.
Part 3 – Substituting expressions into expressions
This question generator allows you to generate questions on the skill of substitution in context of sequences and finding intersection points by solving simultaneous equations by substitution.
Click on a question’s text to reveal the answer.
Teachers: log in to view this content.