This is the students’ version of the page. Log in above for the teachers’ version.
Prerequisites
- G9a – Circle parts – definitions and properties (essential)
- G1e – Conventions for labelling the sides and angles of triangles (essential)
- G3a – Angles at a point, angles at a point on a straight line, vertically opposite angles (essential)
- G3c – The sum of angles in a triangle and the angle properties of polygons (essential)
- G4a – Properties of special triangles and quadrilaterals (essential)
- G17b – Circumference of a circle (desirable)
- G17c – Area of a circle (desirable)
- G18a – Arcs and sectors of circles (desirable)
Circle theorems – interactive GeoGebra applets
Drag points around to see live illustrations of the circle theorems:A triangle formed by two radii and a chord is isosceles
The angle at the centre is double the angle at the circumference
Note that this is true even if the angle at the centre is reflex and even if a chord intersects a radius. Also note that you can click on an angle in this applet to show/hide its value.
The angle in a semicircle is a right angle
This is actually a special case of the theorem about the angle at the centre being double the angle at the circumference:
Angles in the same segment are equal
Note that you can click on an angle in this applet to show/hide its value.
Opposite angles in a cyclic quadrilateral add up to 180º
Cyclic quadrilaterals are four-sided shapes whose corners all lie on the circumference of a circle. Note that you can click on an angle in this applet to show/hide its value.
Make sure that vertices A, B, C and D appear in that order as you go anticlockwise around the circle. Notice that if you drag the vertices so that the order is e.g. A, C, B, D, you will no longer have a quadrilateral.
The angle between a tangent and radius is 90º
Two tangents from a common point to two points on the circle are the same length
With thanks to Michael Borcherds, whose Common Tangents to a Circle applet is available here. Material modified and embedded here under the CC-BY-SA 3.0 license.
The perpendicular line from the centre of the circle to a chord bisects the chord
>
With thanks to Adam Antonio, whose Chord Properties 1 applet is available here. Material modified and embedded here under the CC-BY-SA 3.0 license.
The angle between a tangent and chord is equal to the angle in the alternate segment
Note that you can click on an angle in this applet to show/hide its value.
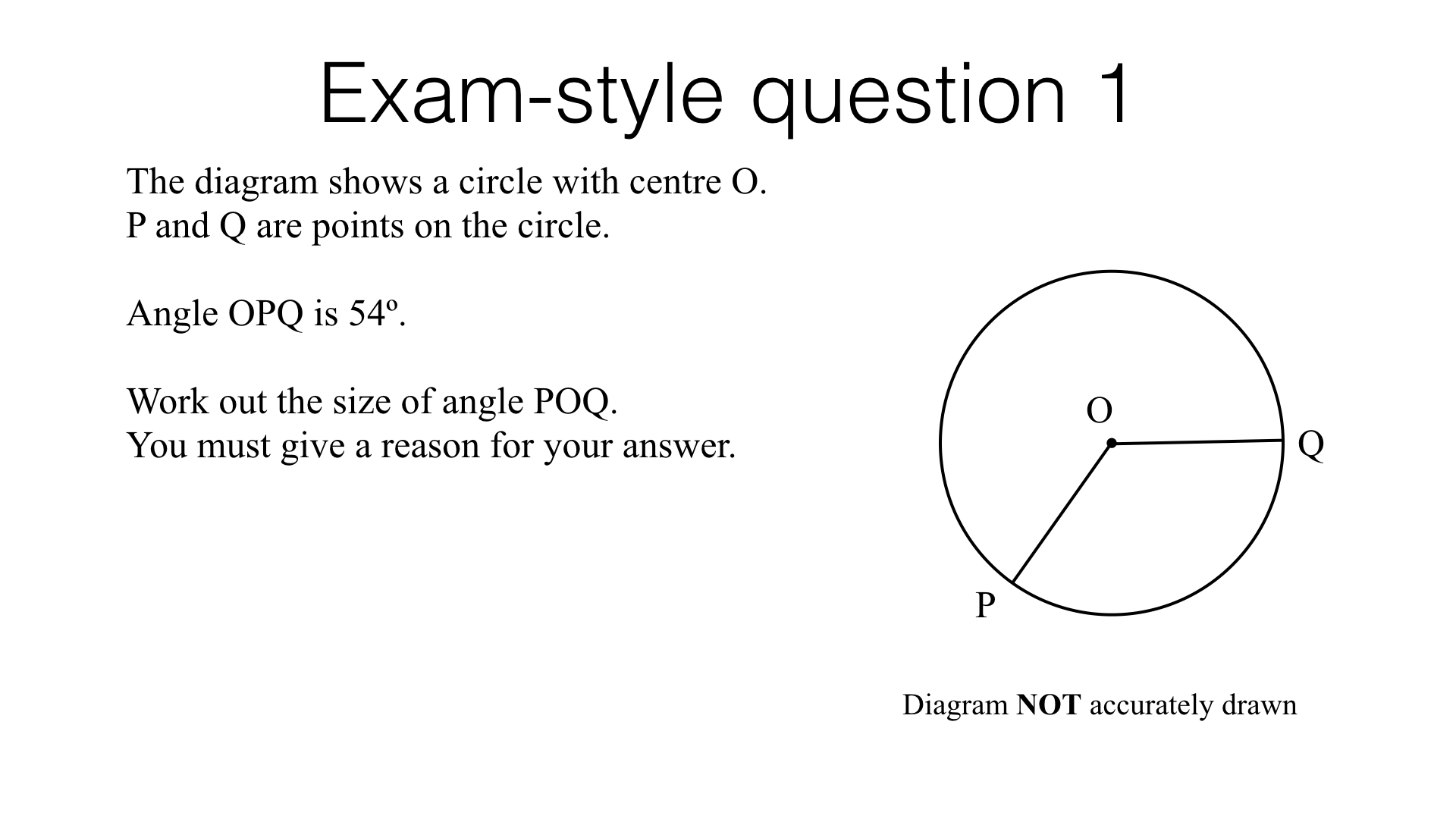
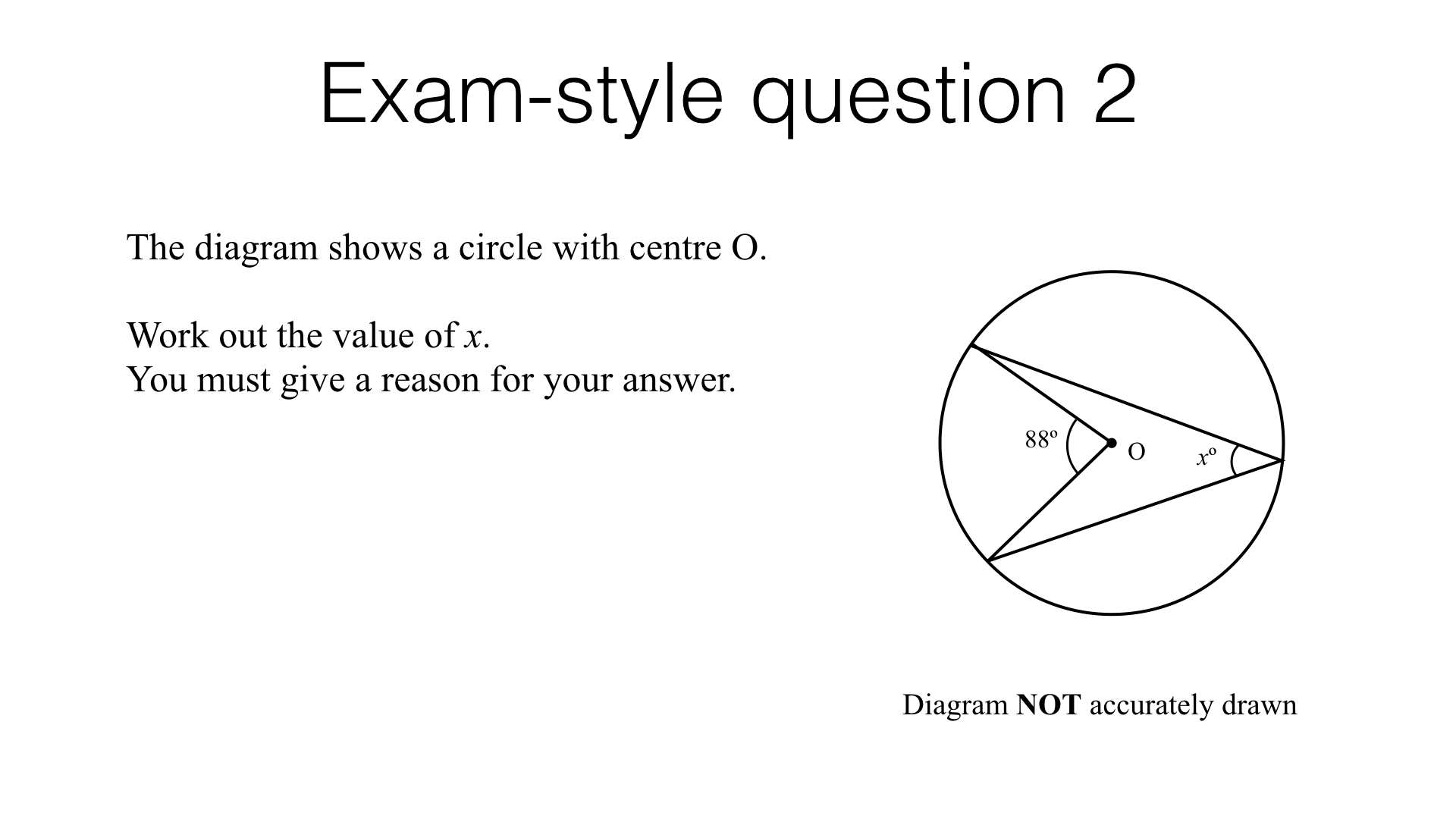
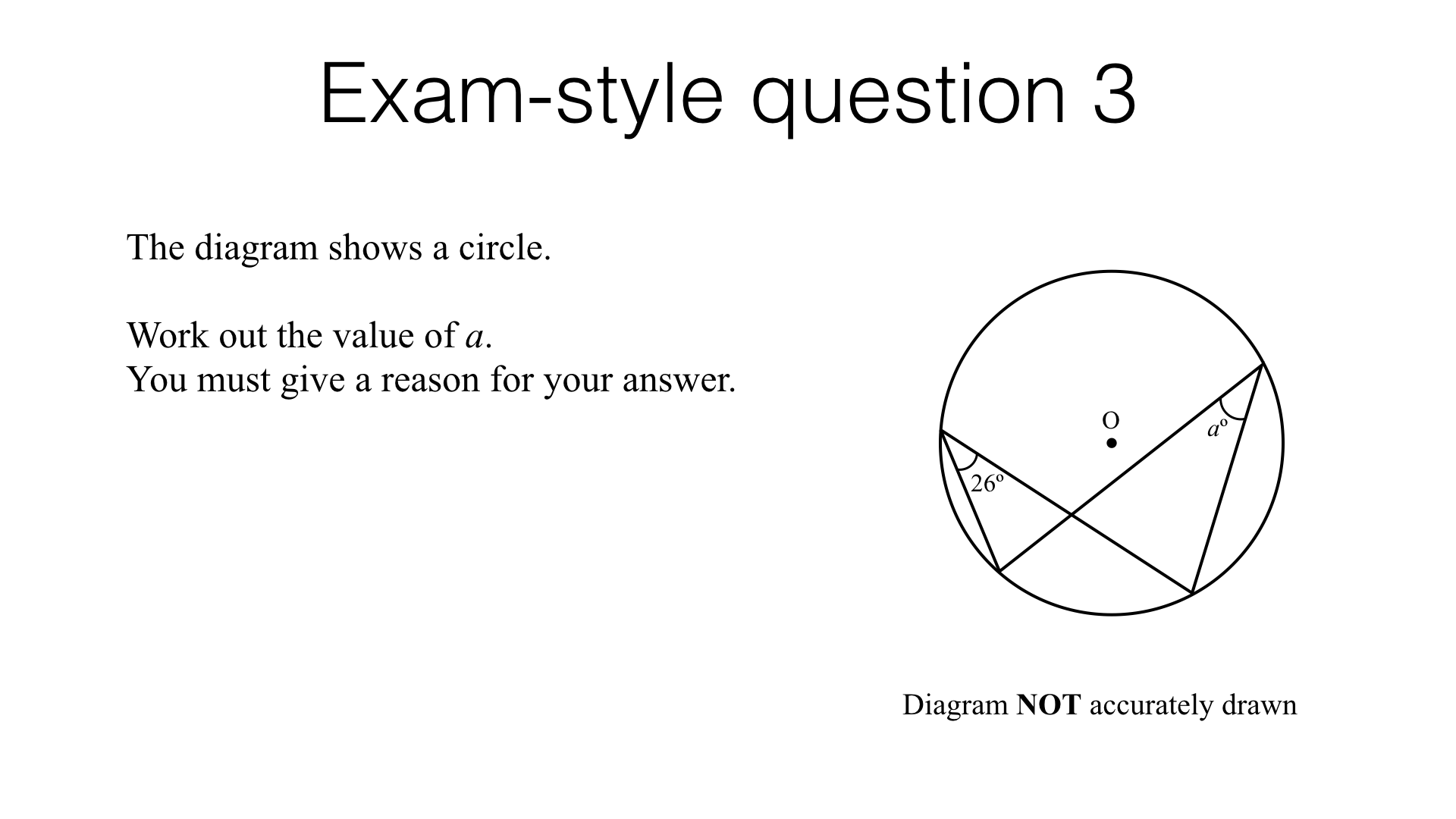
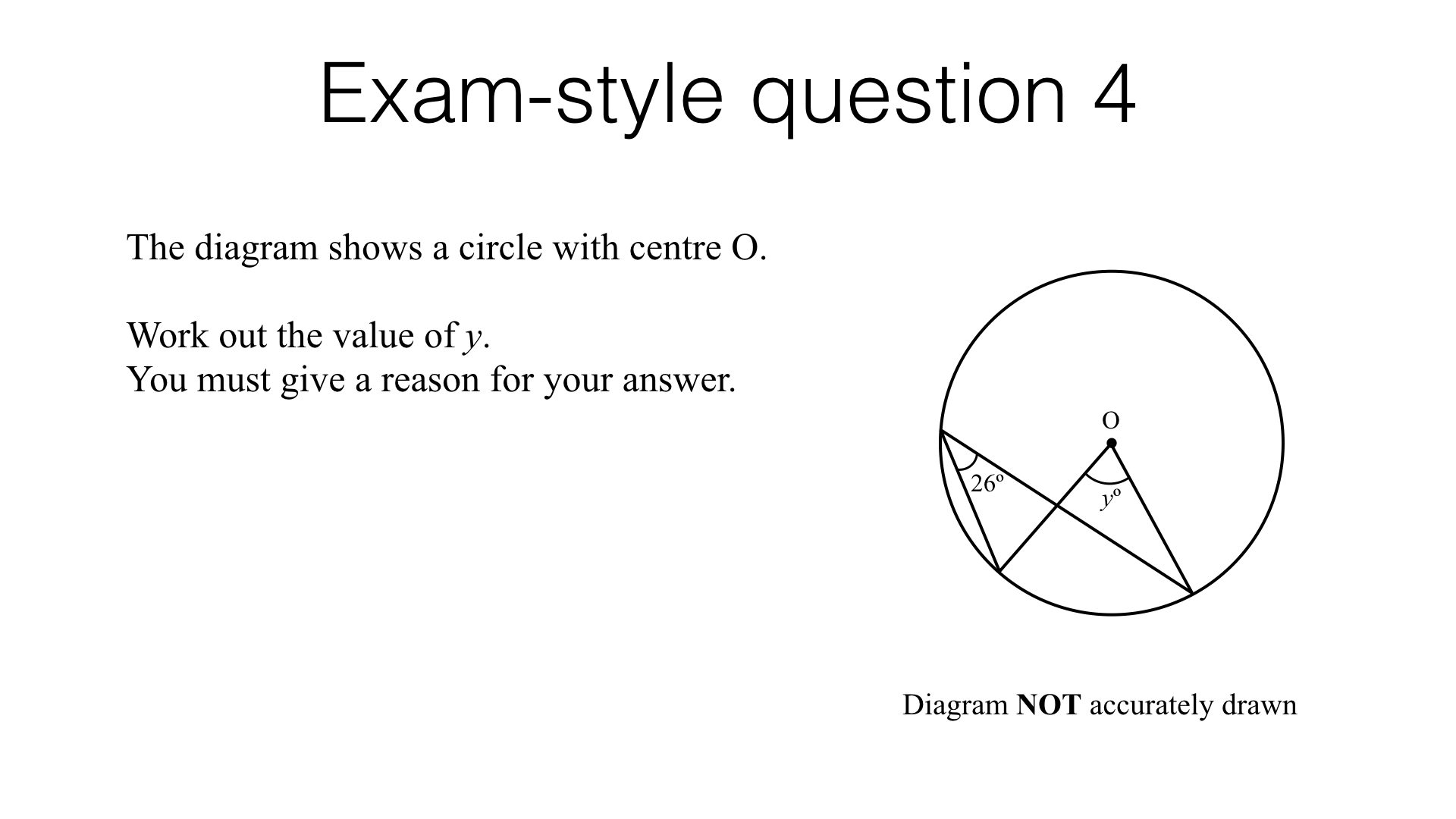
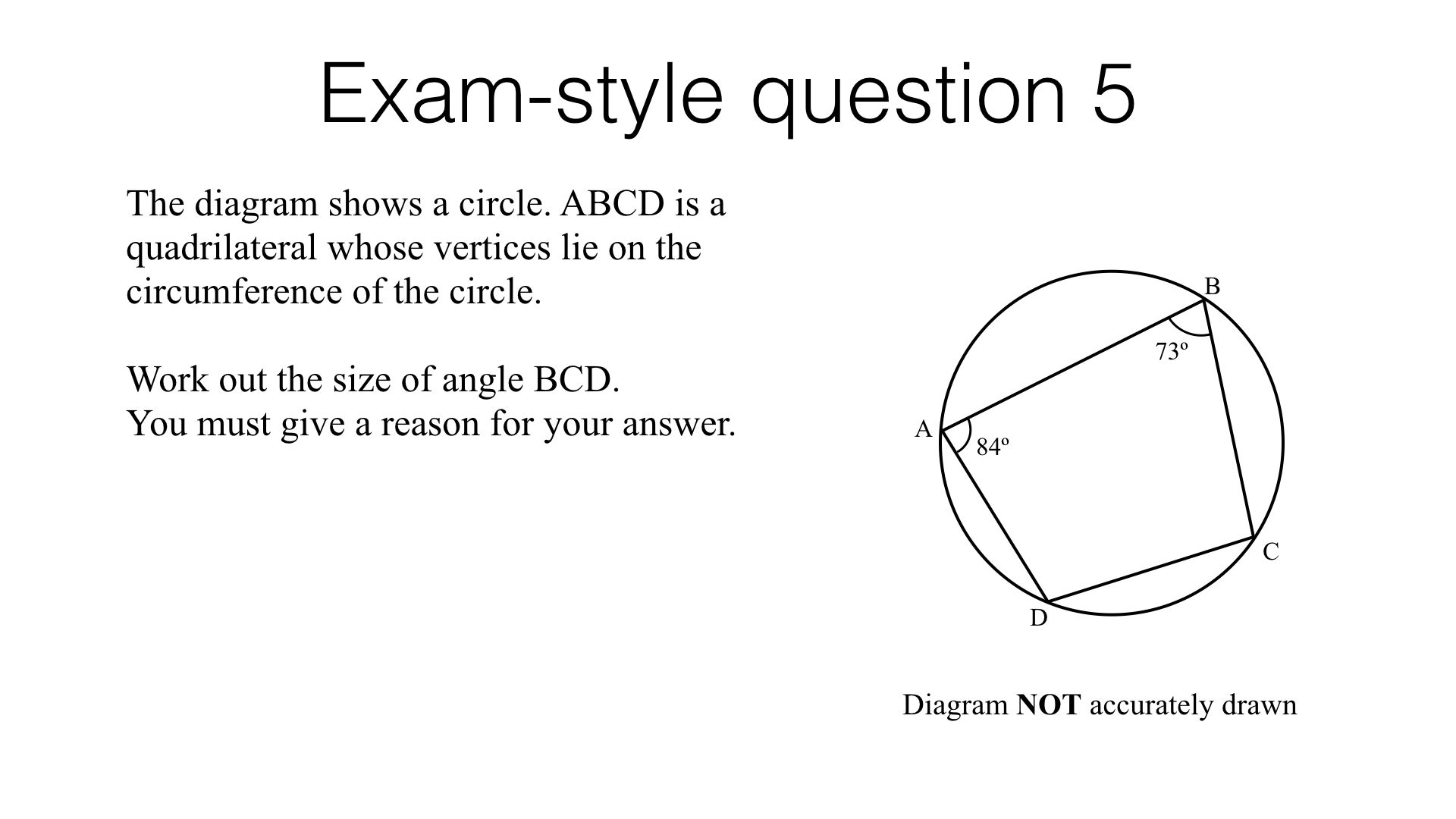
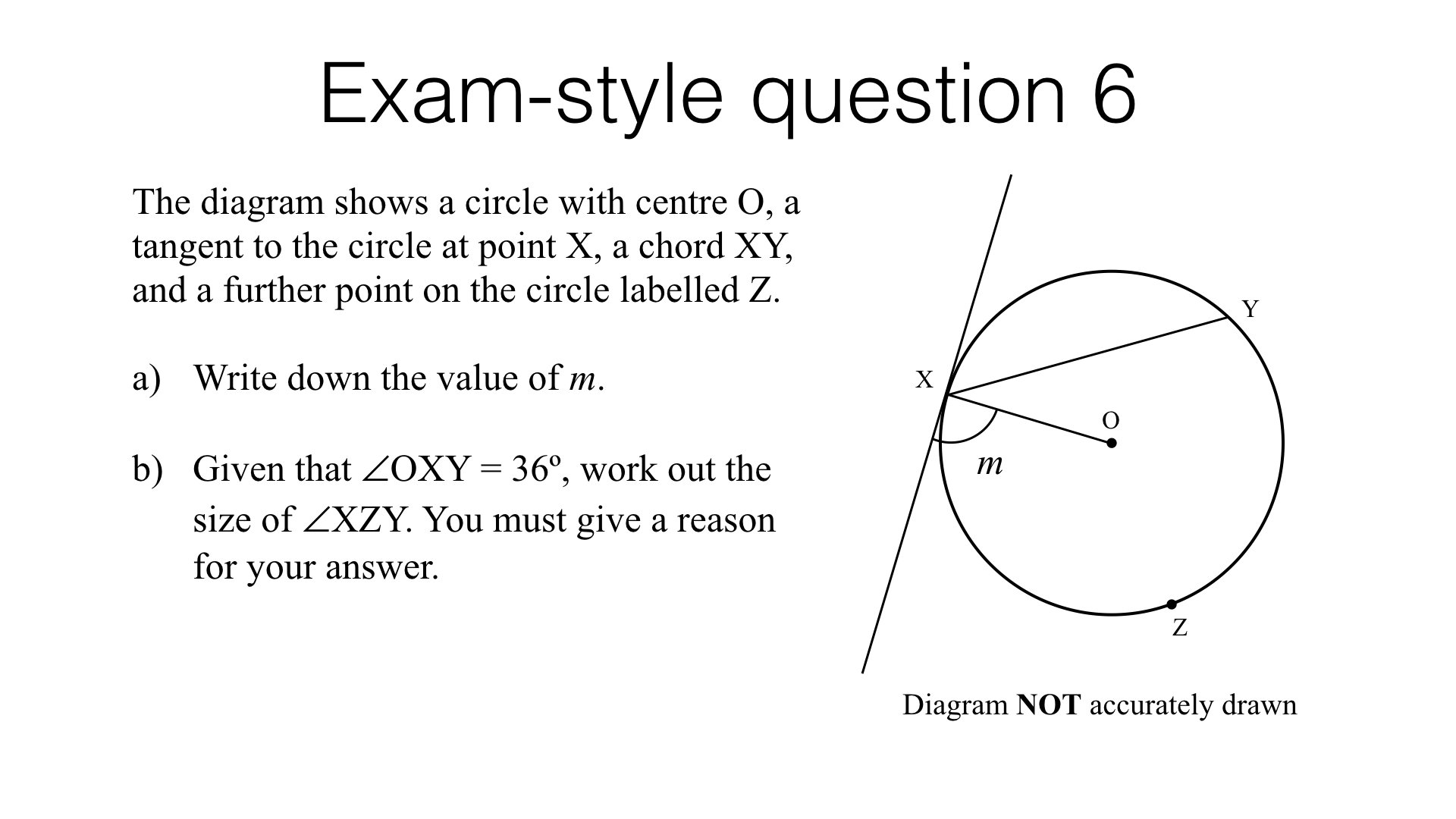
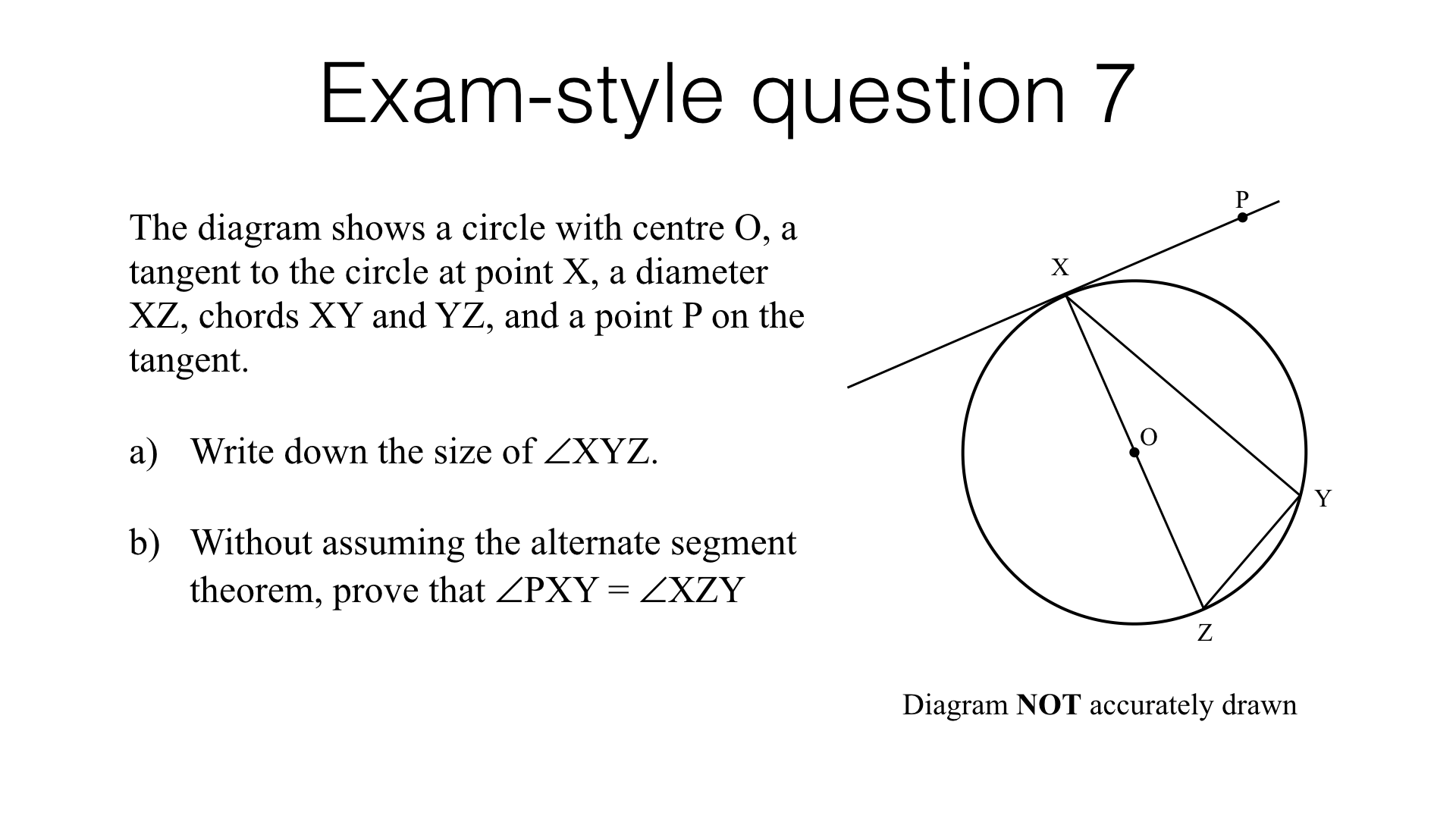
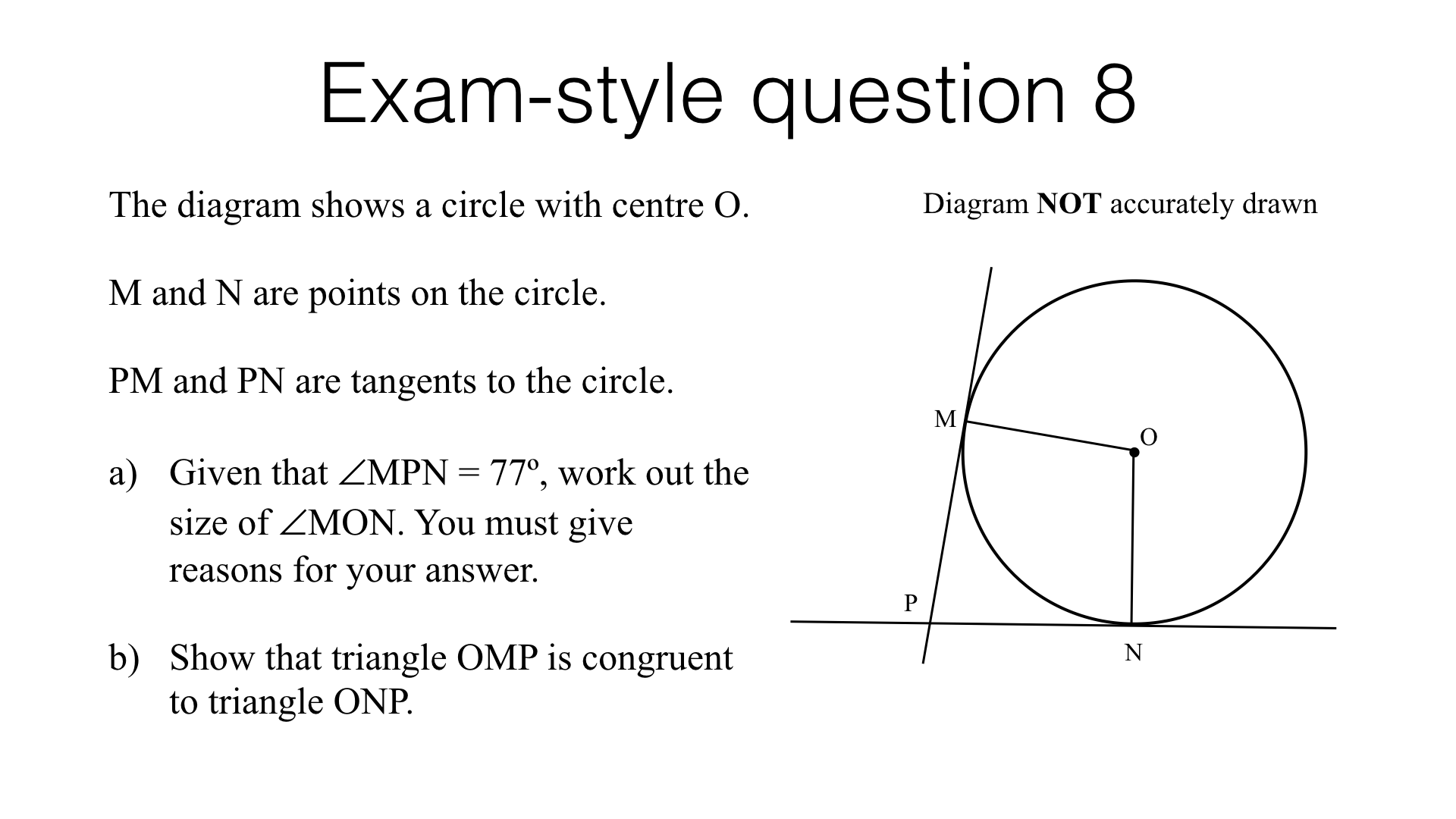
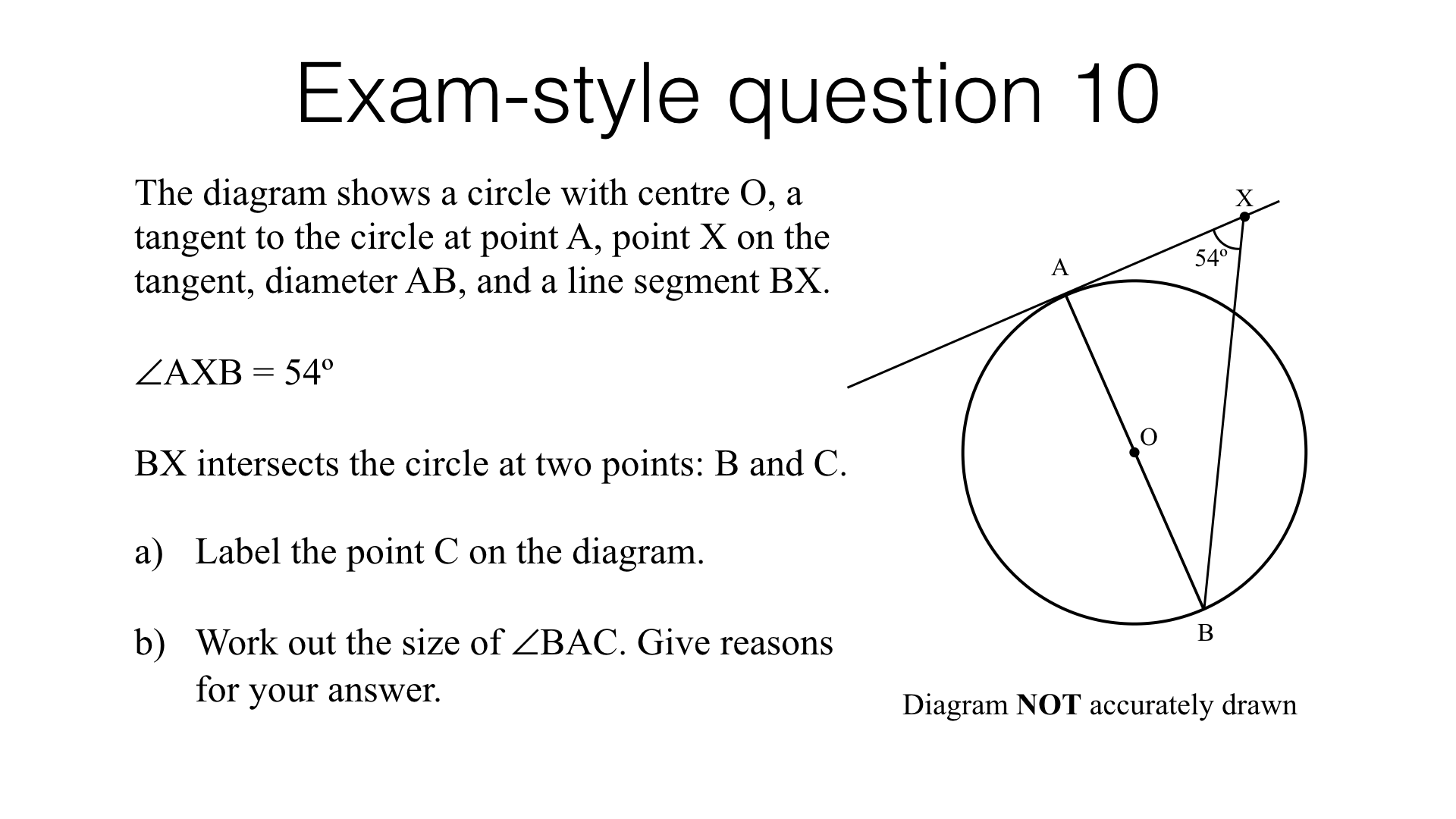
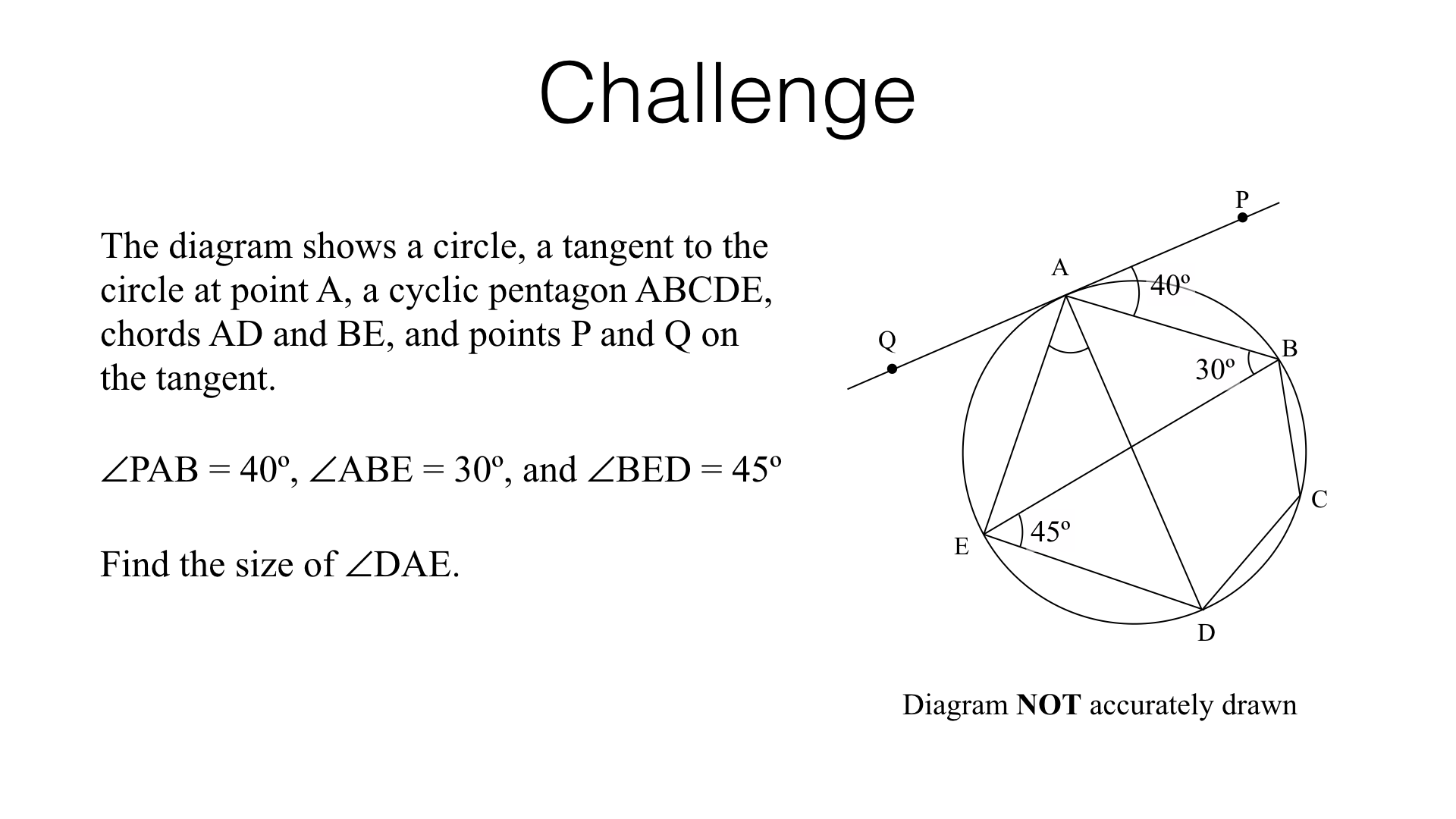
Circle theorems – exam-style questions
Teacher resources
Teachers: log in to access the following:
- Slides in PPTX (with click-to-reveal answers)
- Slides in PDF (one slide per page, suitable for importing into IWB software)
- Worksheet (with space for student work)
- Handout (slides with exercises only; 4 per page for reduced printing)
- Goal-free version of this lesson
- Handout (slides with exercises only; 4 per page for reduced printing)
Links to past exam questions
Teachers: log in to access these.
Circle theorems: applying a given theorem to a diagram in more than one way
Worksheet for this task (Login required)
In the real world
Teachers: log in to view this content.