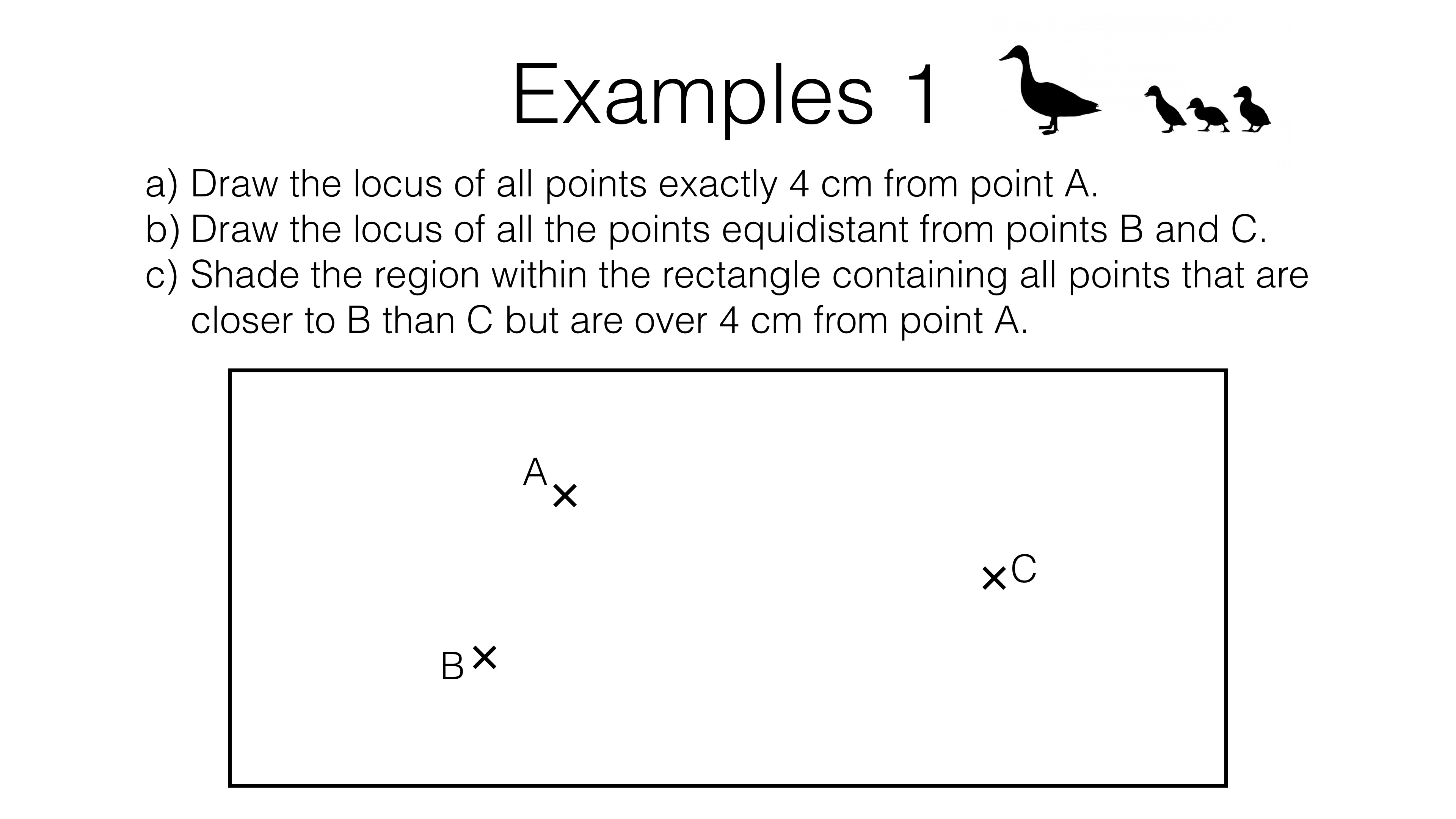
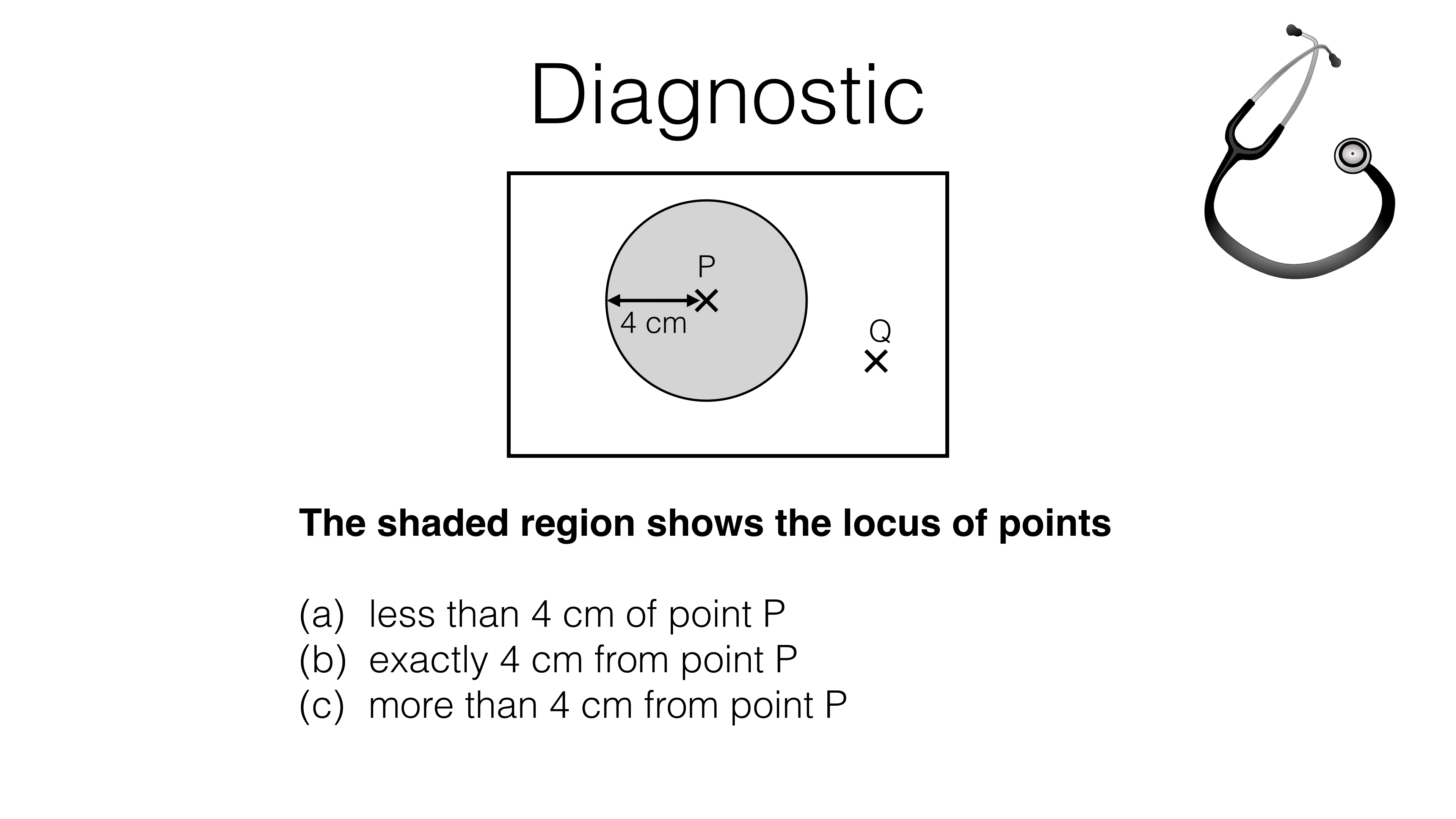
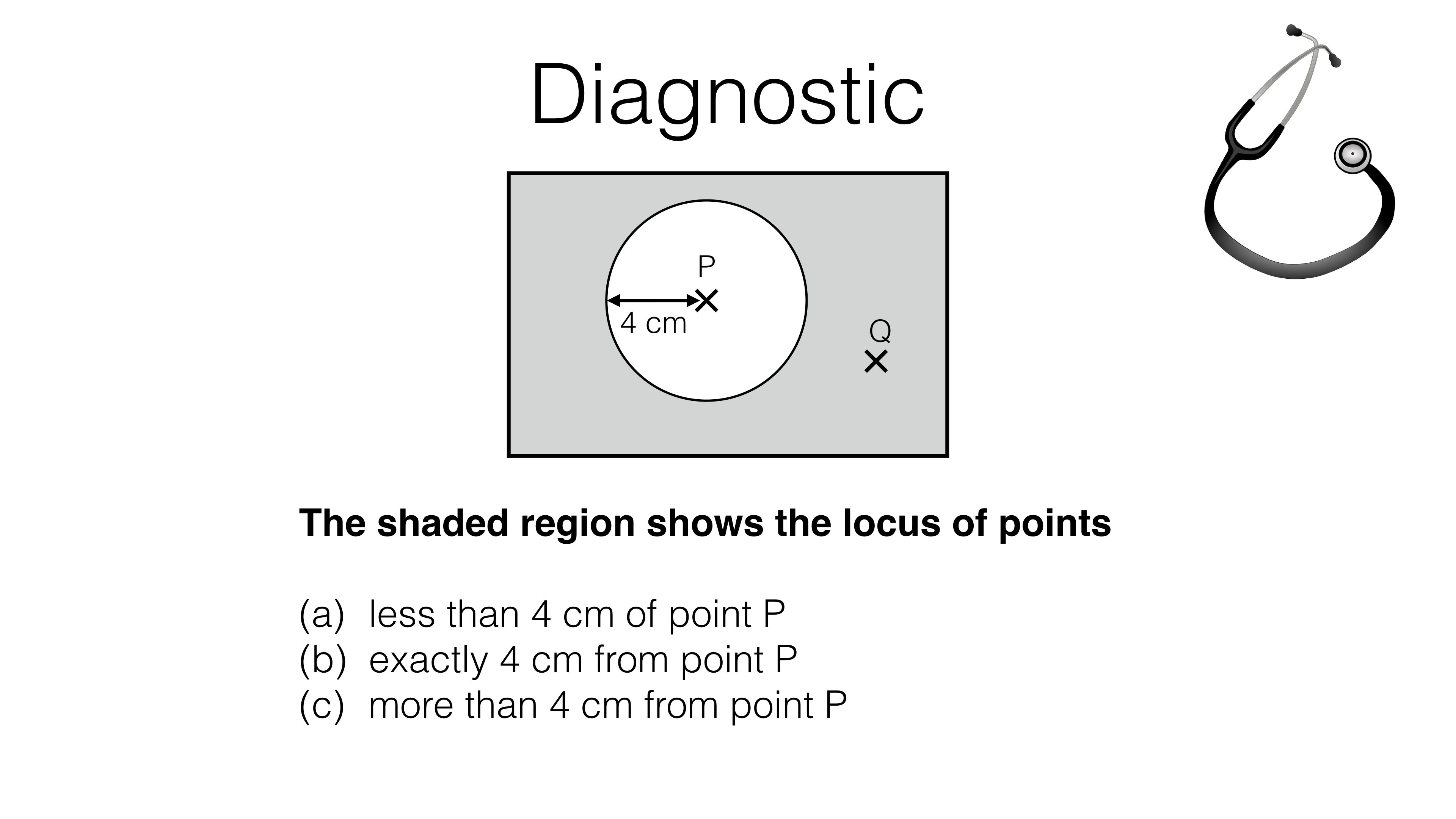
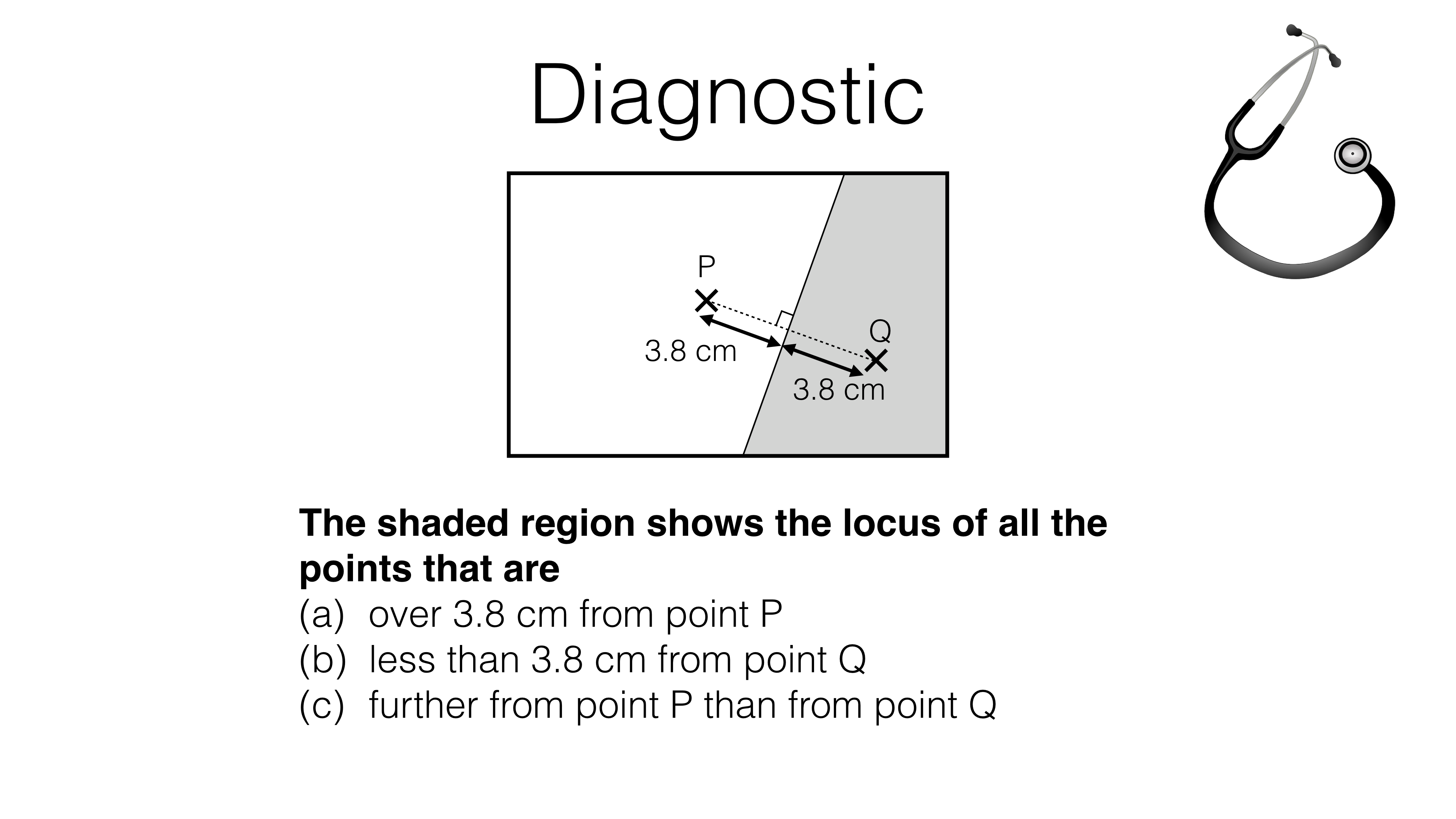
This is the students’ version of the page. Log in above for the teachers’ version.
- G2a – Constructing perpendicular bisectors, angle bisectors, and perpendiculars to or from a point
- R2a – Using scale diagrams and maps and/or G15b – Scale drawings
- G2b – Constructing triangles (required for the Challenge question)
A starting point
A fixed distance from a point
Drag the red point so that it is 5 m from A. The point will turn blue when you have done so, and it will leave a blue mark on the canvas. Move the point to different position that is also 5 m from A. Keep doing this. Try to drag the point along all the possible locations that are 5 m from A:
Equidistant from two points
Drag the red point so that it is the same distance away from A and B. The point will turn blue when you have done so, and it will leave a blue mark on the canvas. Move the point to different position that is also equidistant from A and B. Keep doing this. Try to drag the point along all the possible locations:
A fixed distance from a line segment
Drag the red point so that it is 5 m from the line segment AB. The point will turn blue when you have done so, and it will leave a blue mark on the canvas. Move the point to different position that is also 5 m from AB. Keep doing this. Try to drag the point along all the possible locations that are 5 m from AB:
Mixed loci problems
This lesson is different from most BossMaths lessons. It only contains worked examples, diagnostic questions, exam-style questions and a challenge. The worksheet (available under Teacher resources to registered schools only) is required for this lesson, as the diagrams are formatted to print at the appropriate size on A4 paper.Teachers: log in to access the following:
- Worksheet (with space for student work)
Teachers: log in to access these.
Interactive activity: Identifying loci
Identify the locus shown in the diagram. Click “New question” to generate a new diagram and “Show answer” to reveal the answer. Click the toggle to choose between easy and harder questions. Note that the dashed straight line in the harder questions is the perpendicular bisector of AB.
Teachers: log in to view this content.