This is the students’ version of the page. Log in above for the teachers’ version.
- G7a – Coordinates
- A9a – Plotting straight line graphs (required for Part 2)
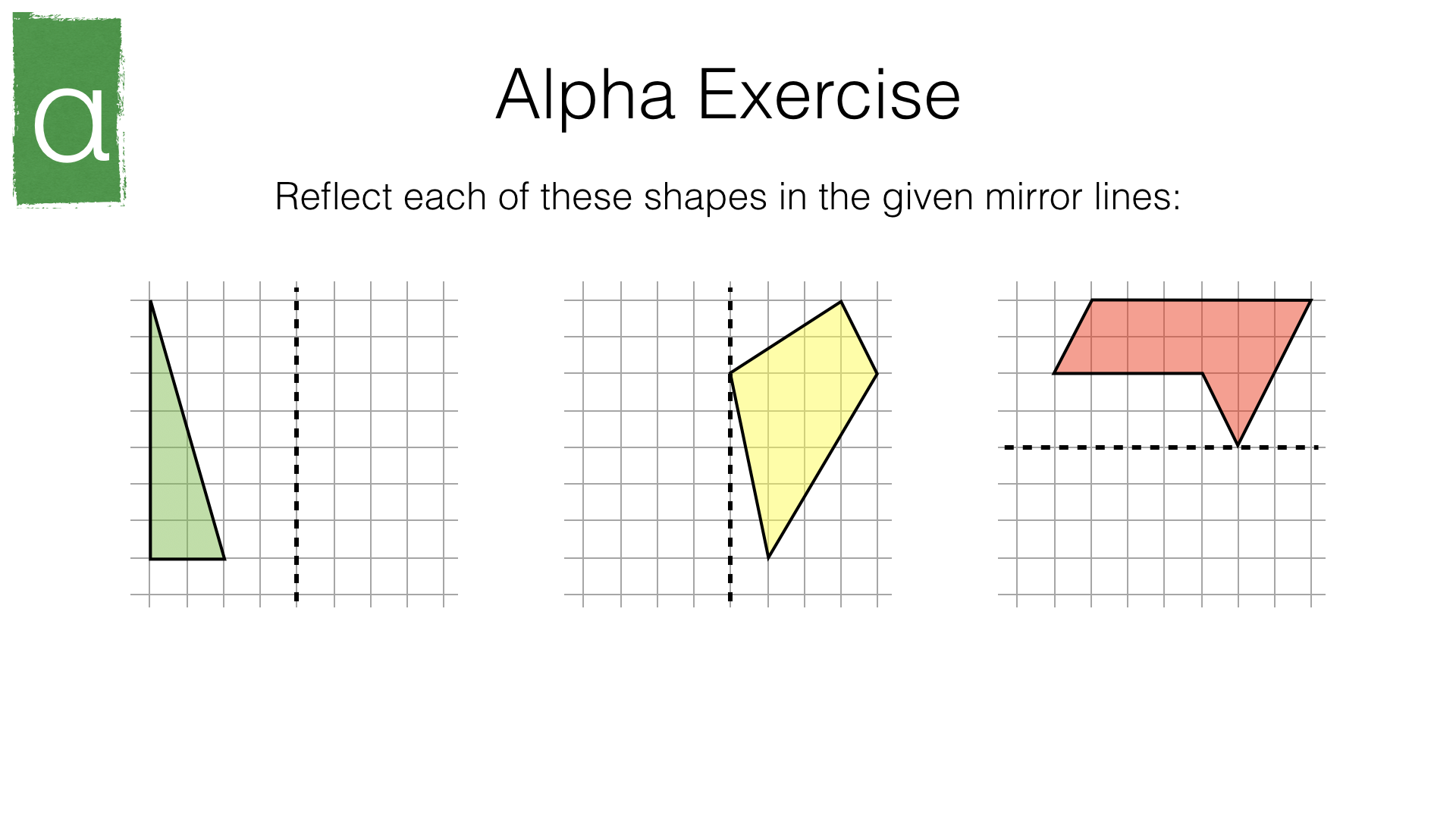
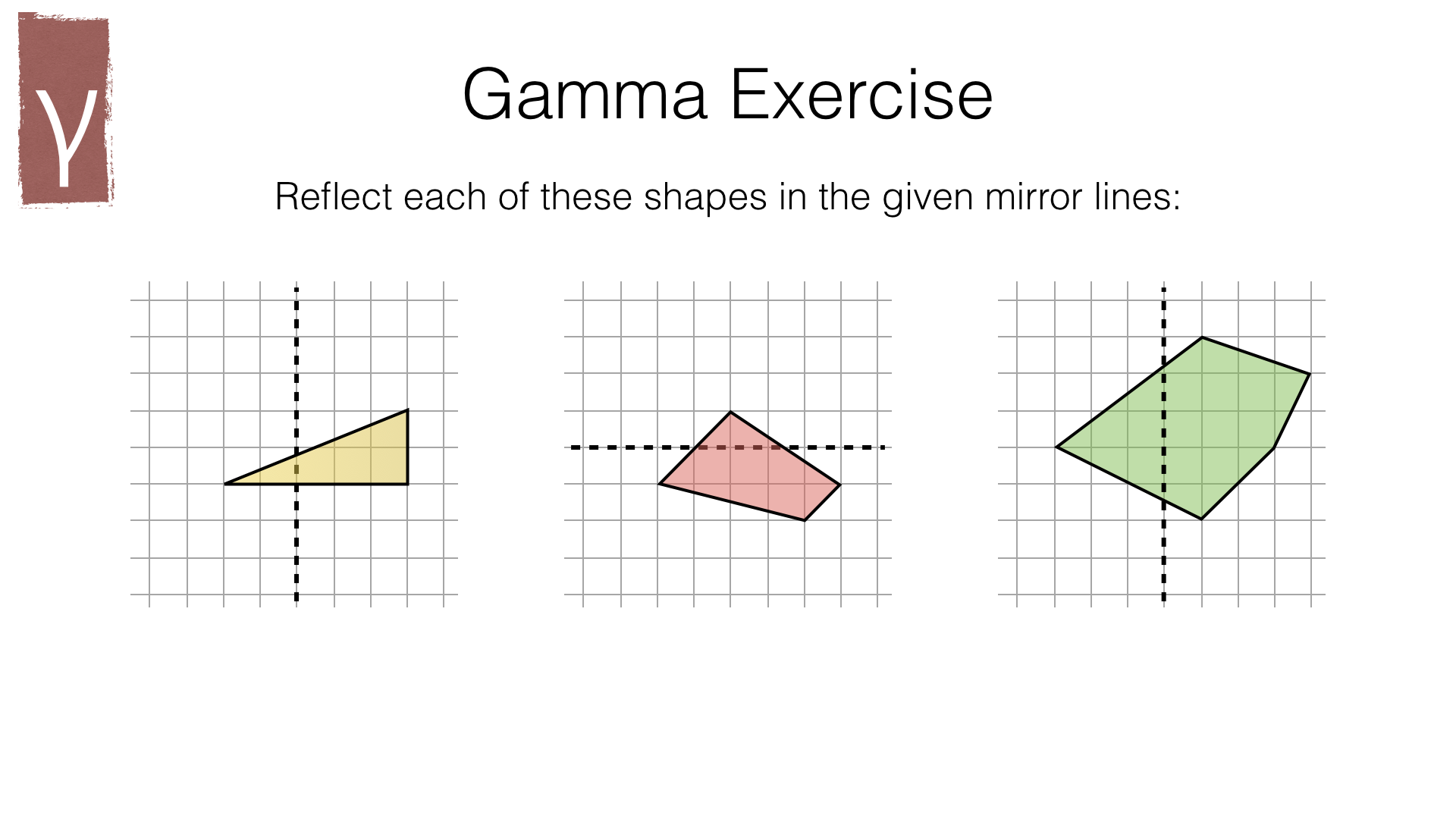
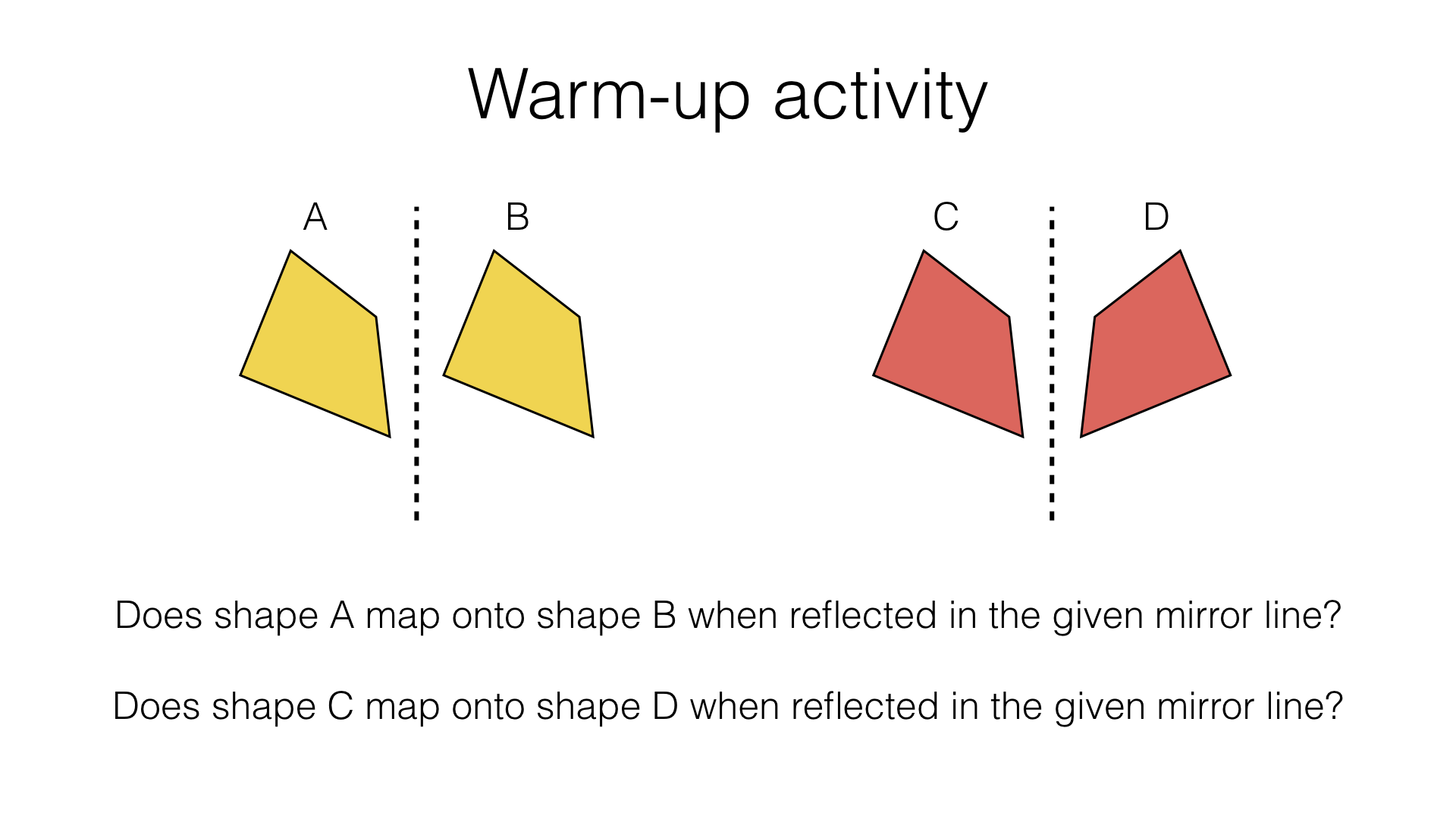
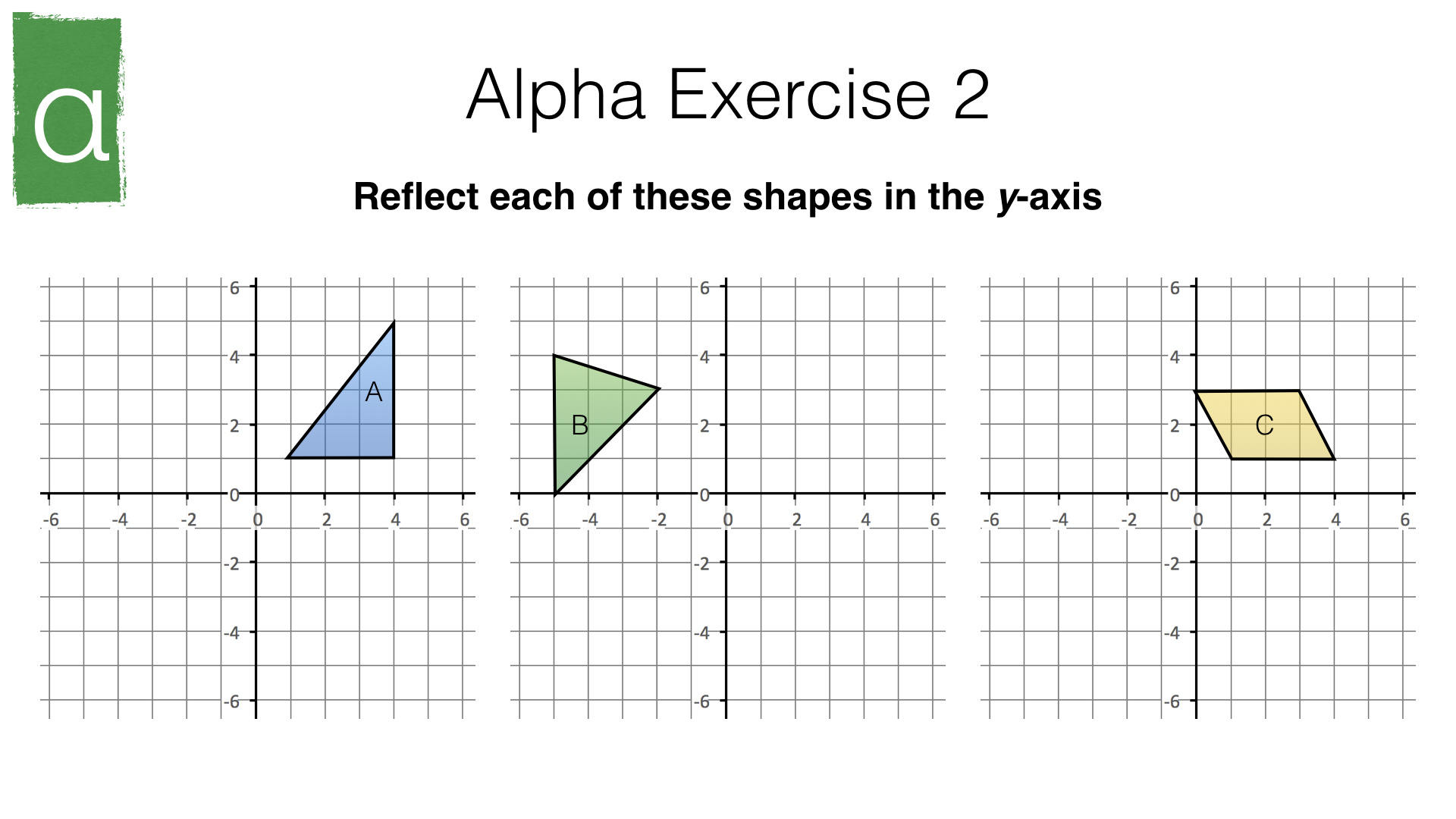
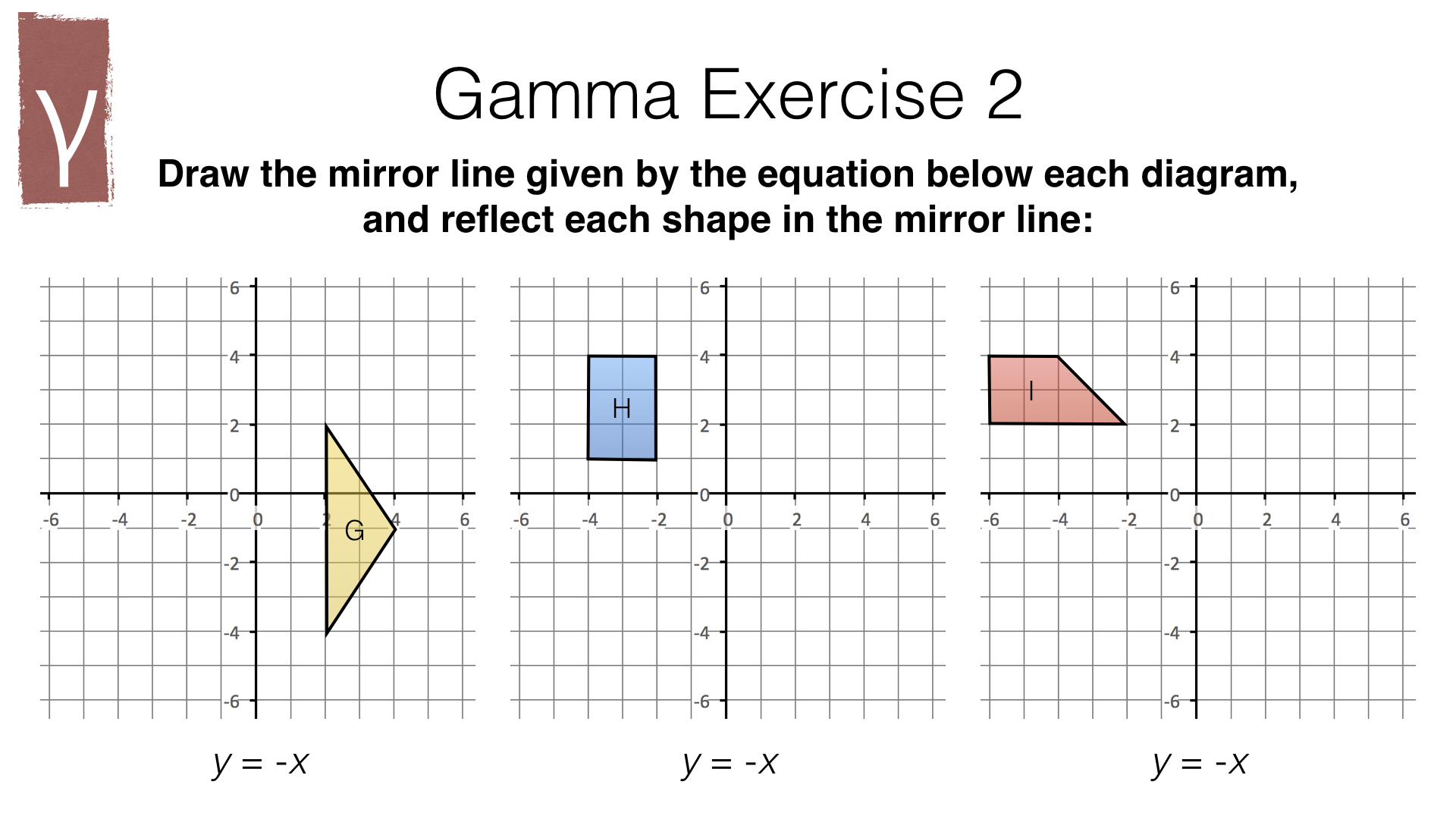
Part 1 – Reflection (easy)
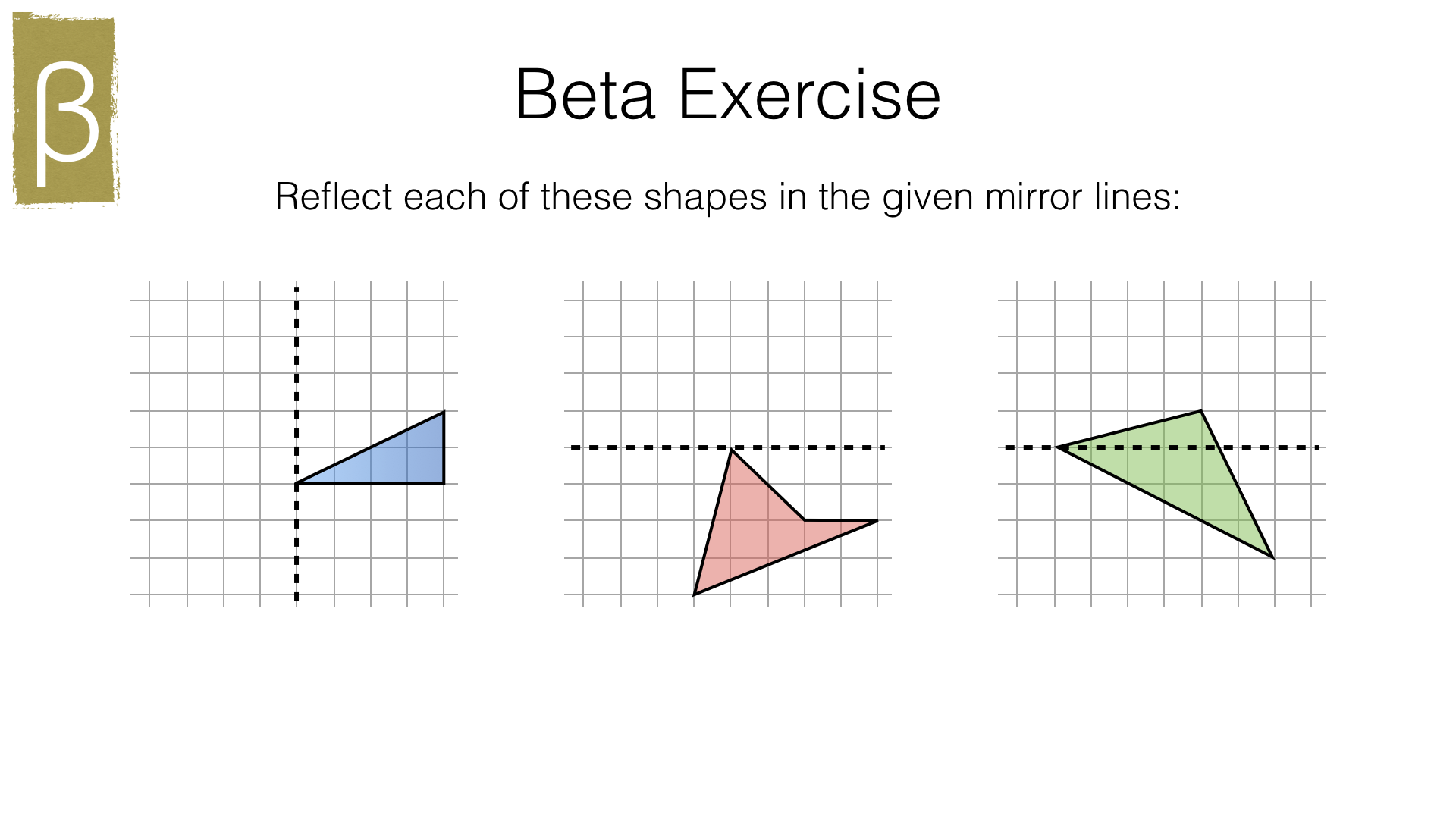
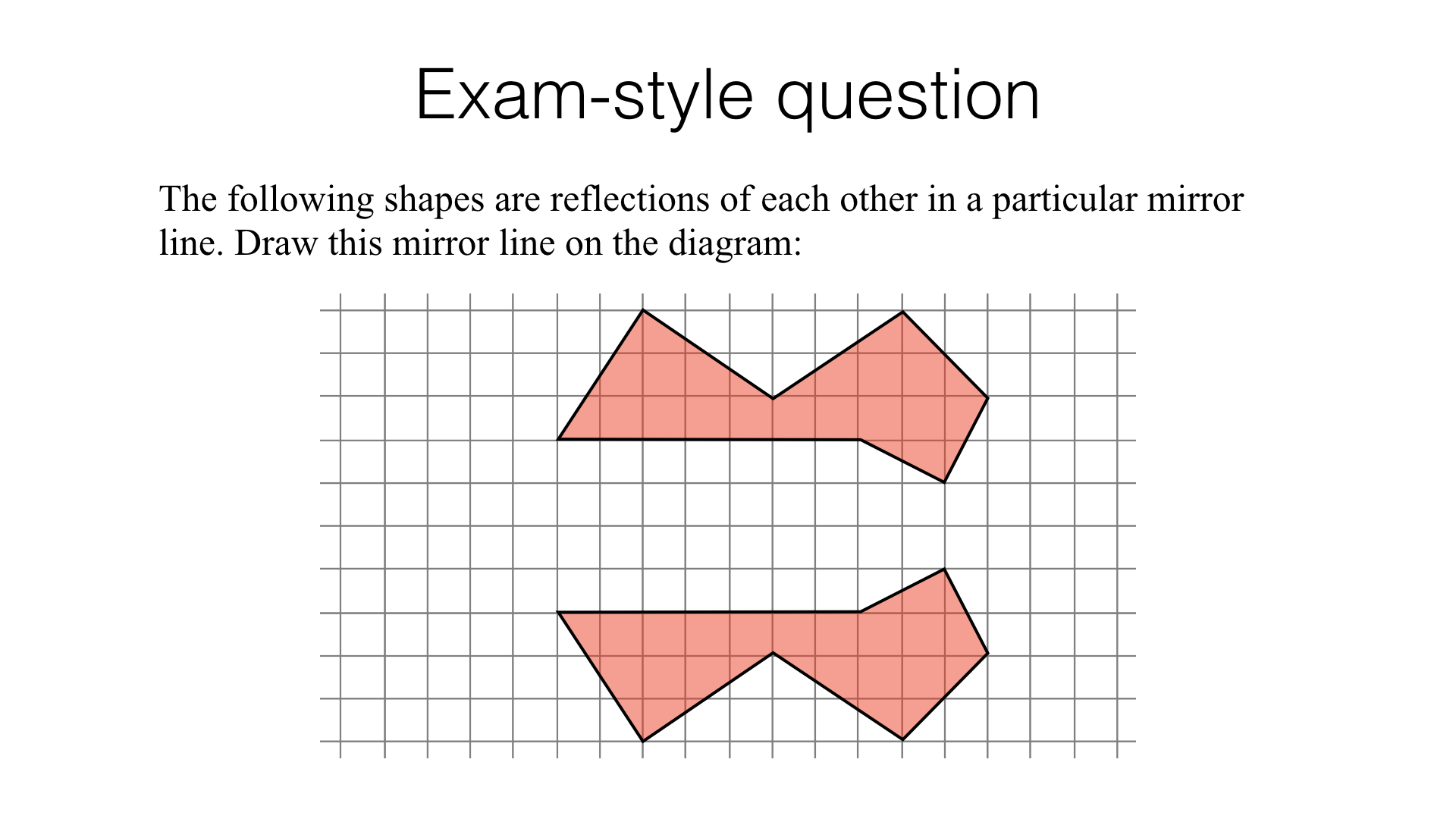
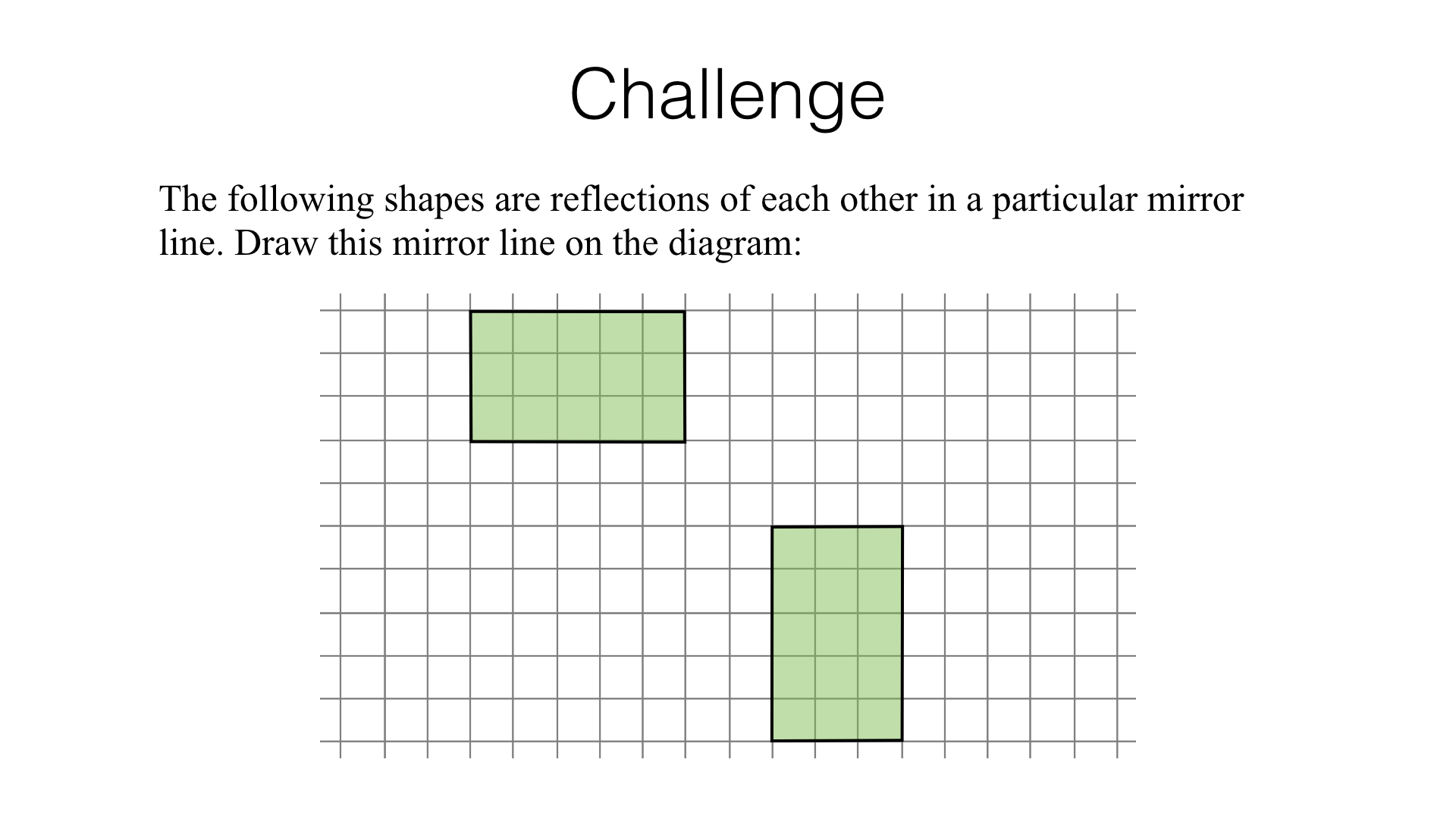
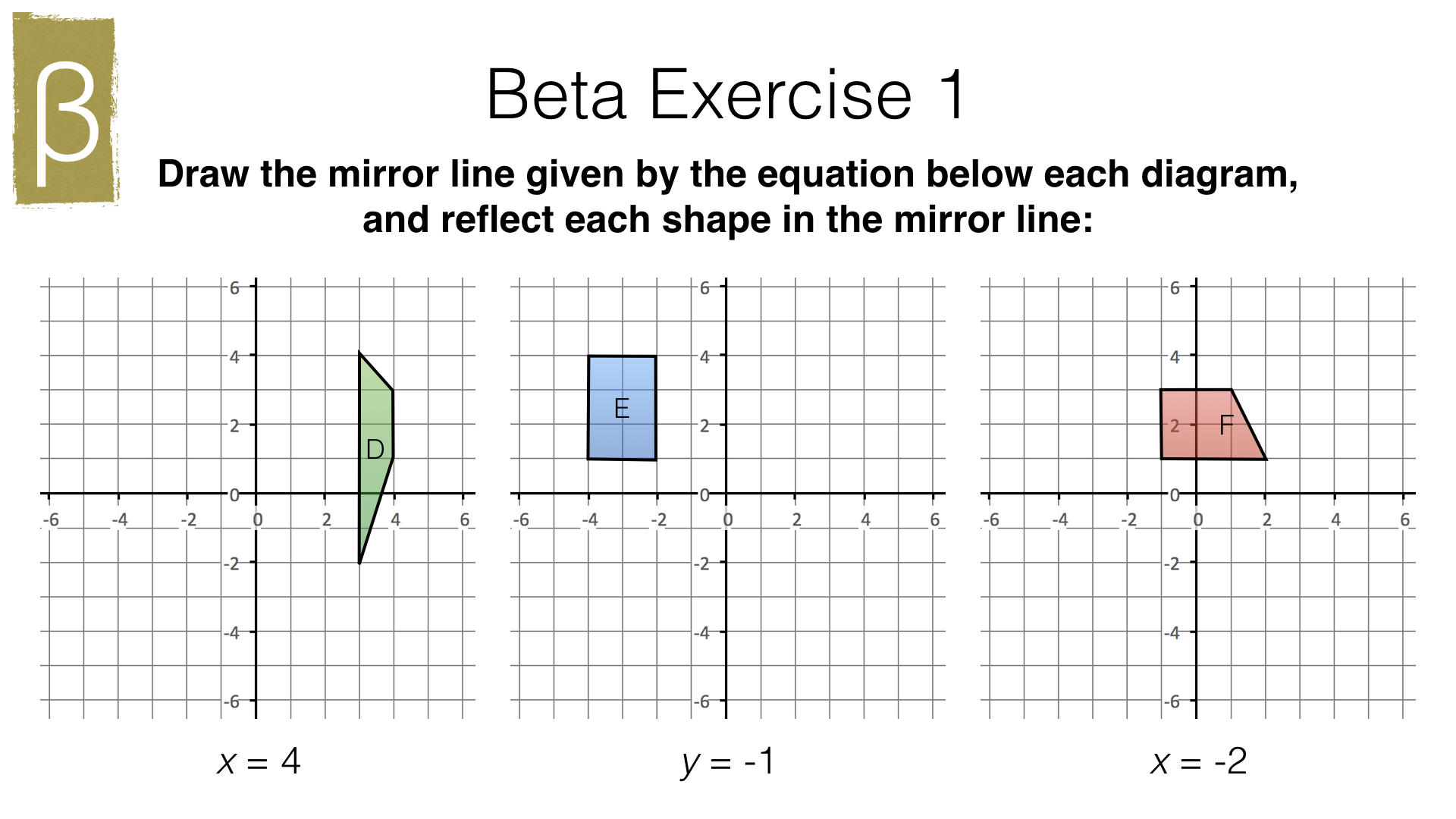
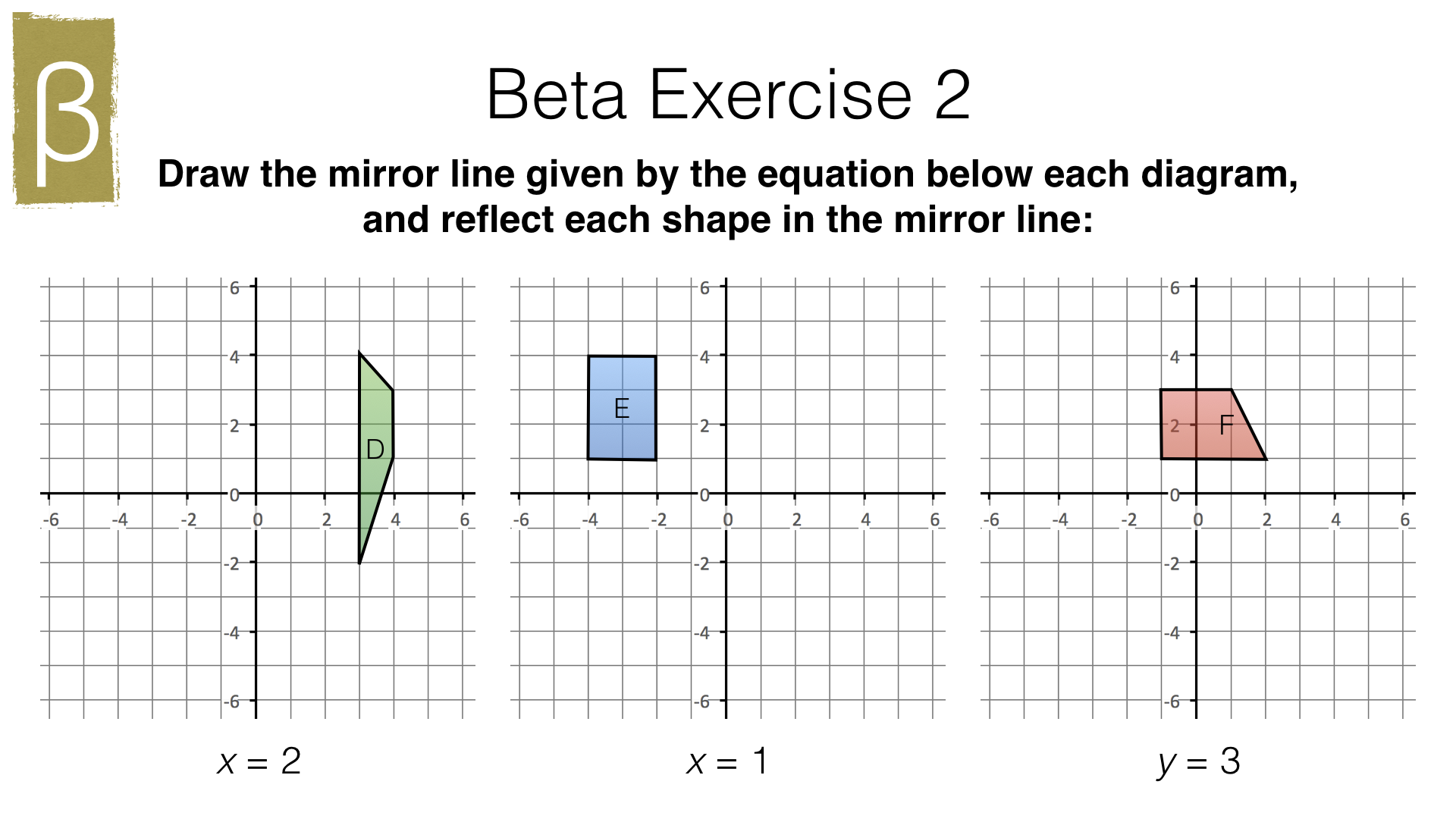
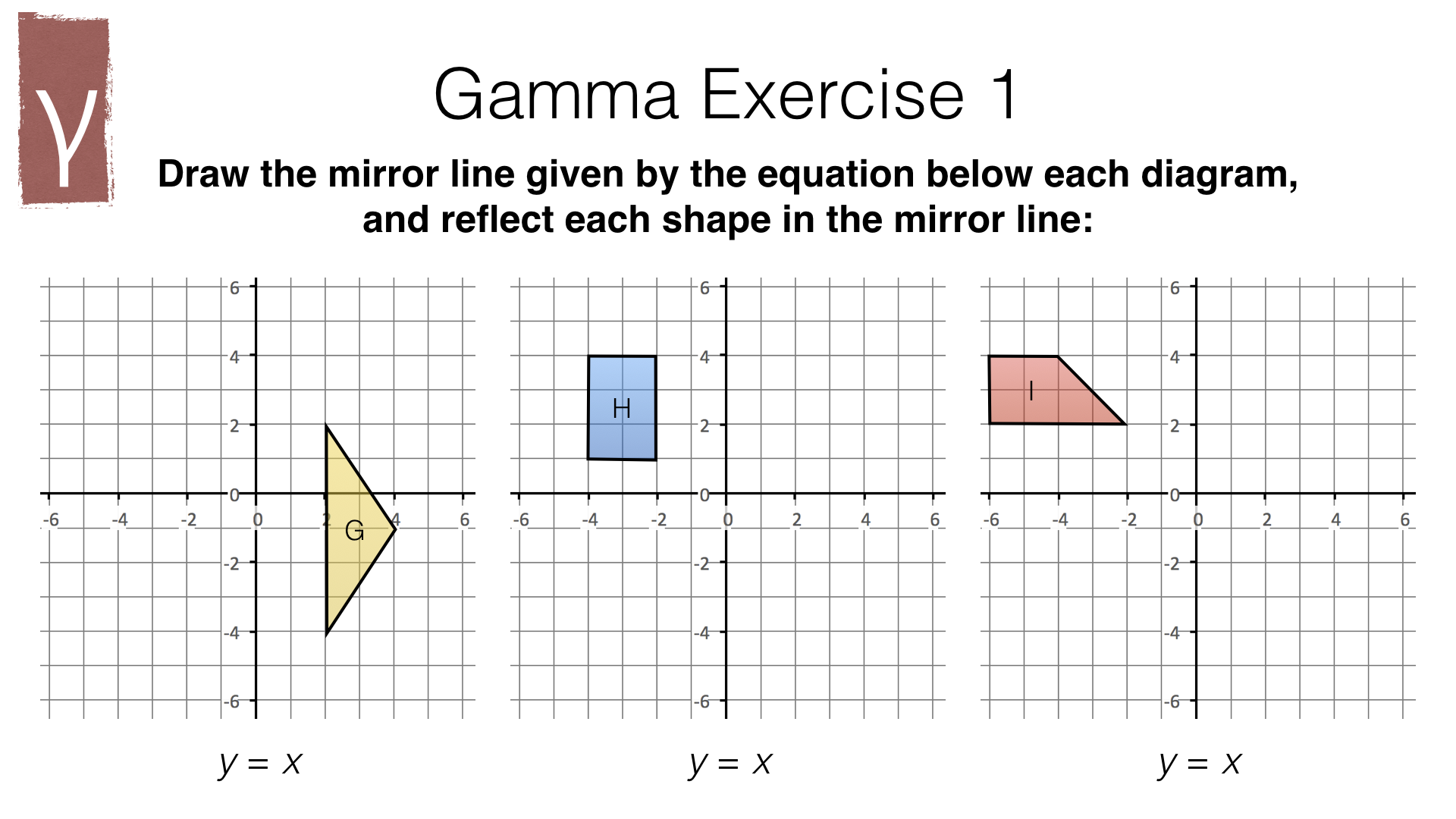
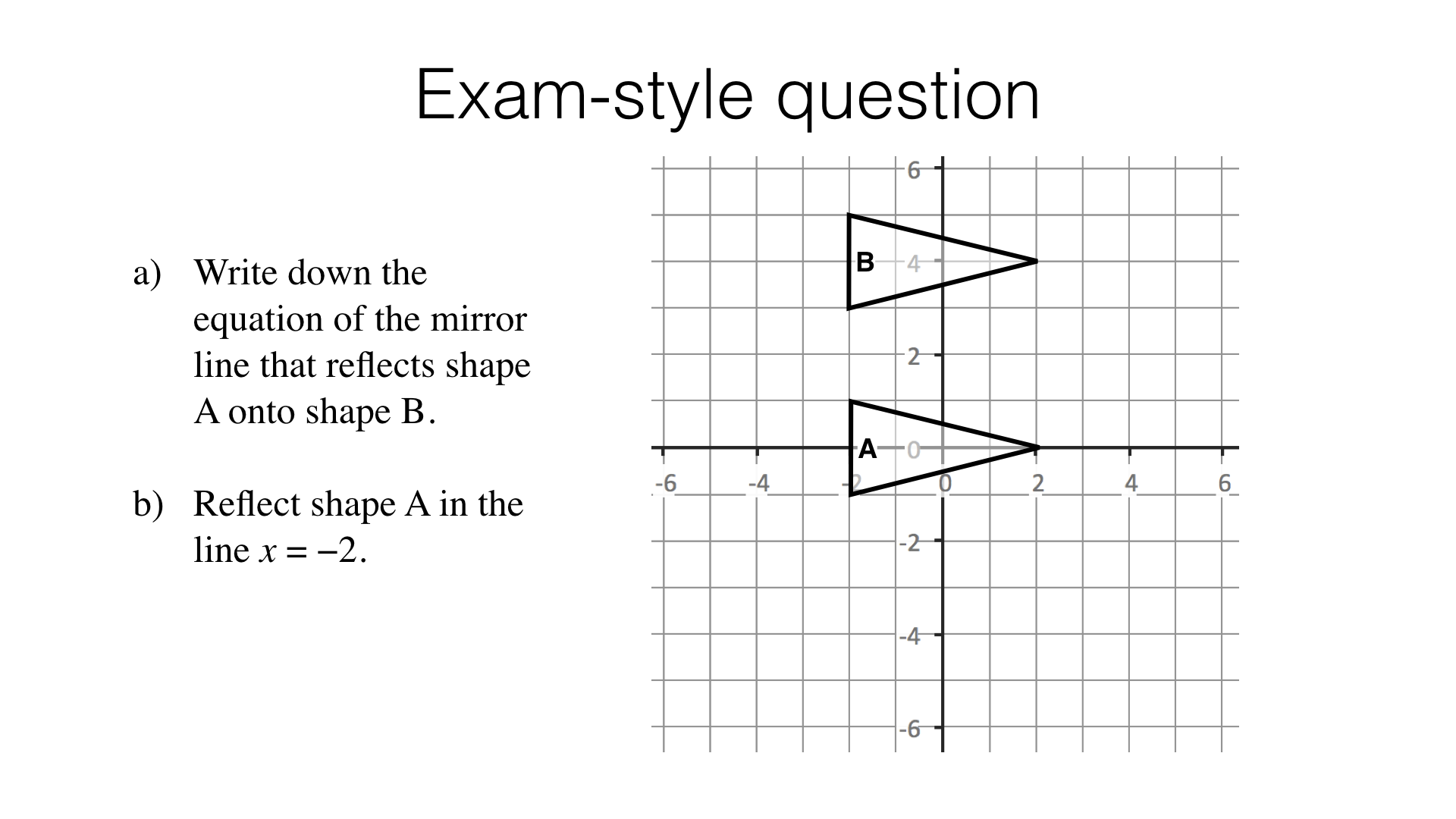
Part 2 – Reflection (hard)
- A reflection maps \((x,y)\) to \((-x,y)\). What is the reflection?
- A reflection maps \((x,y)\) to \((x,-y)\). What is the reflection?
- A reflection maps \((x,y)\) to \((y,x)\). What is the reflection?
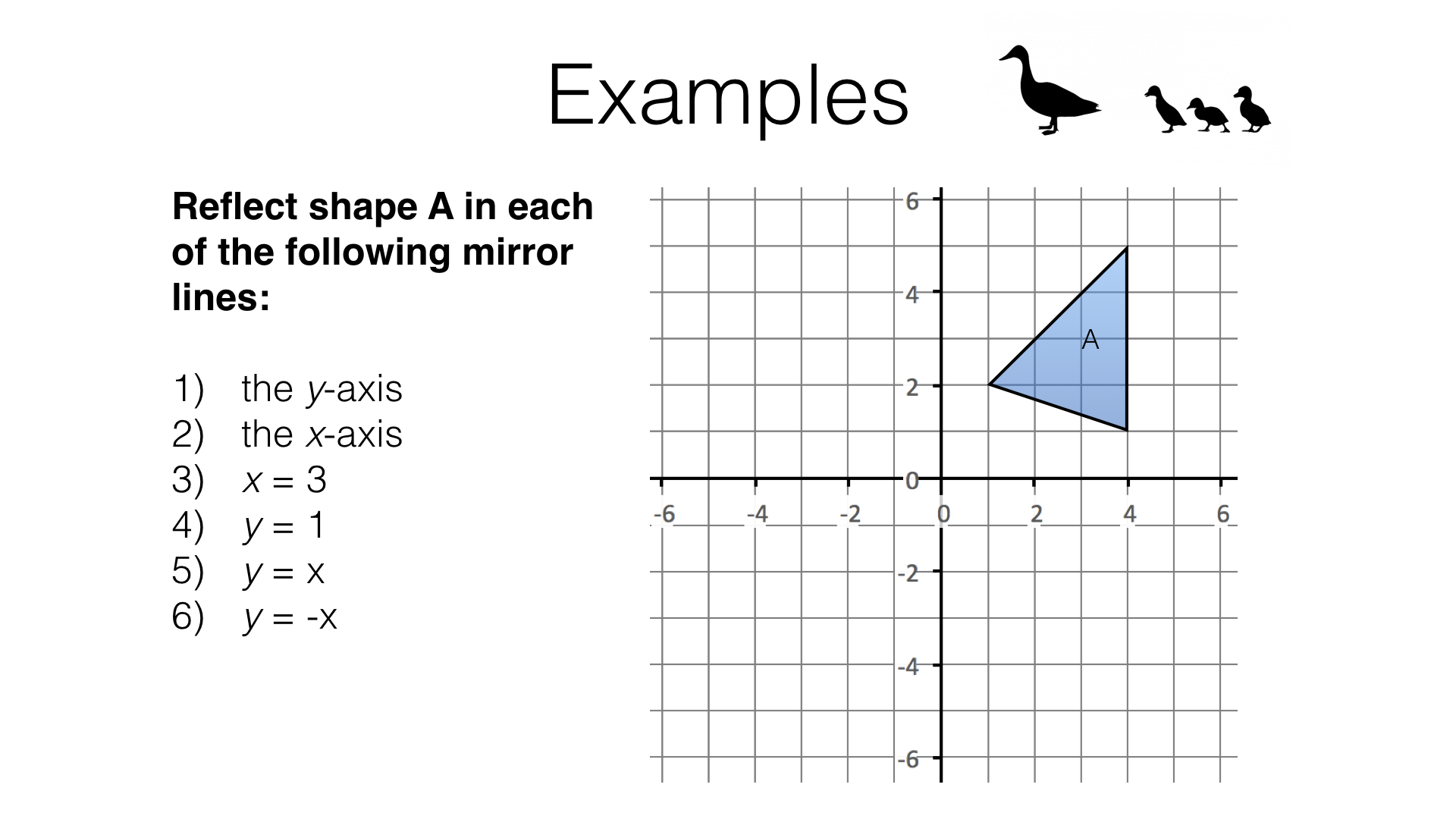
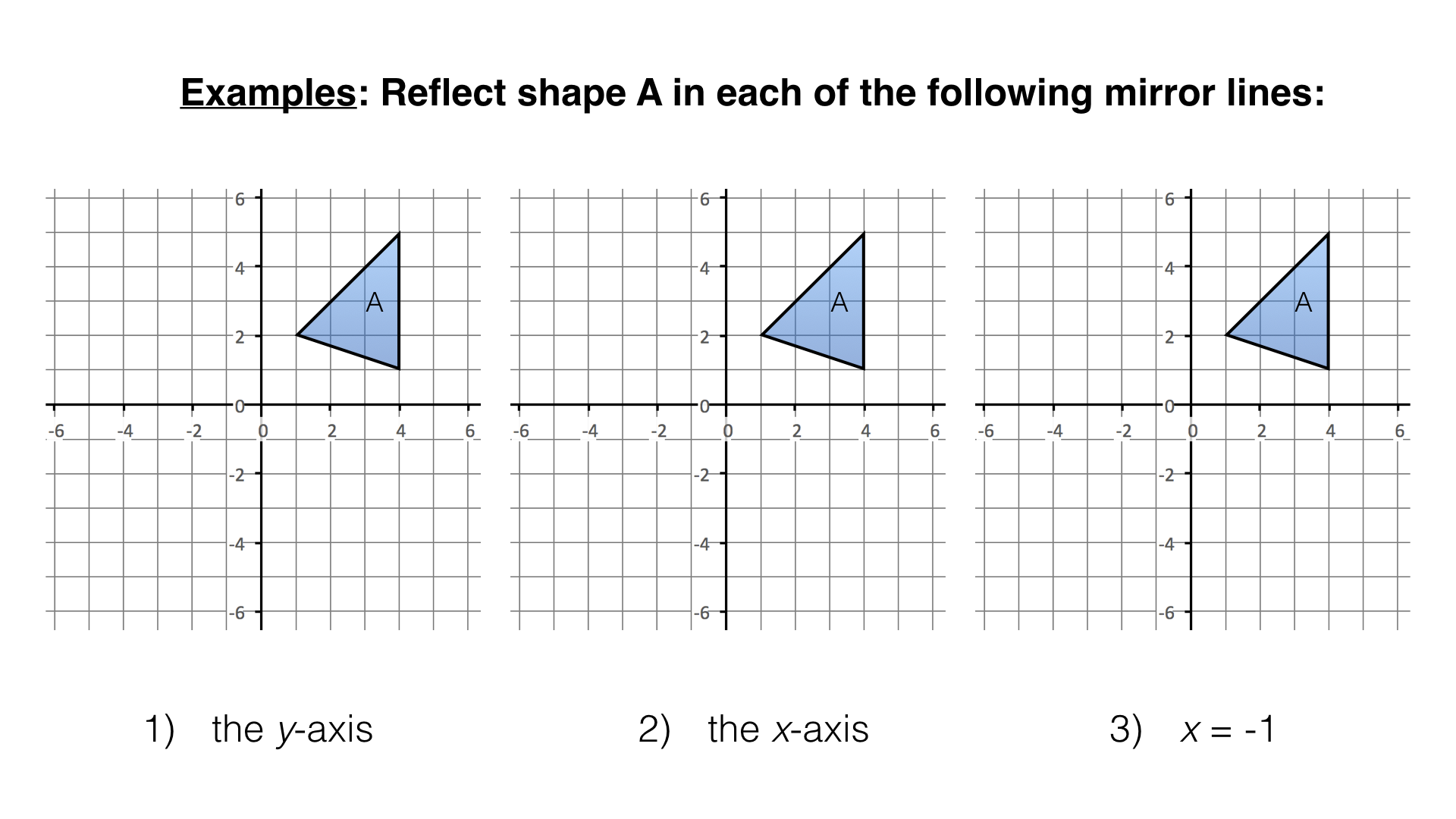
- Reflection in the y-axis or the line \(x=0\)
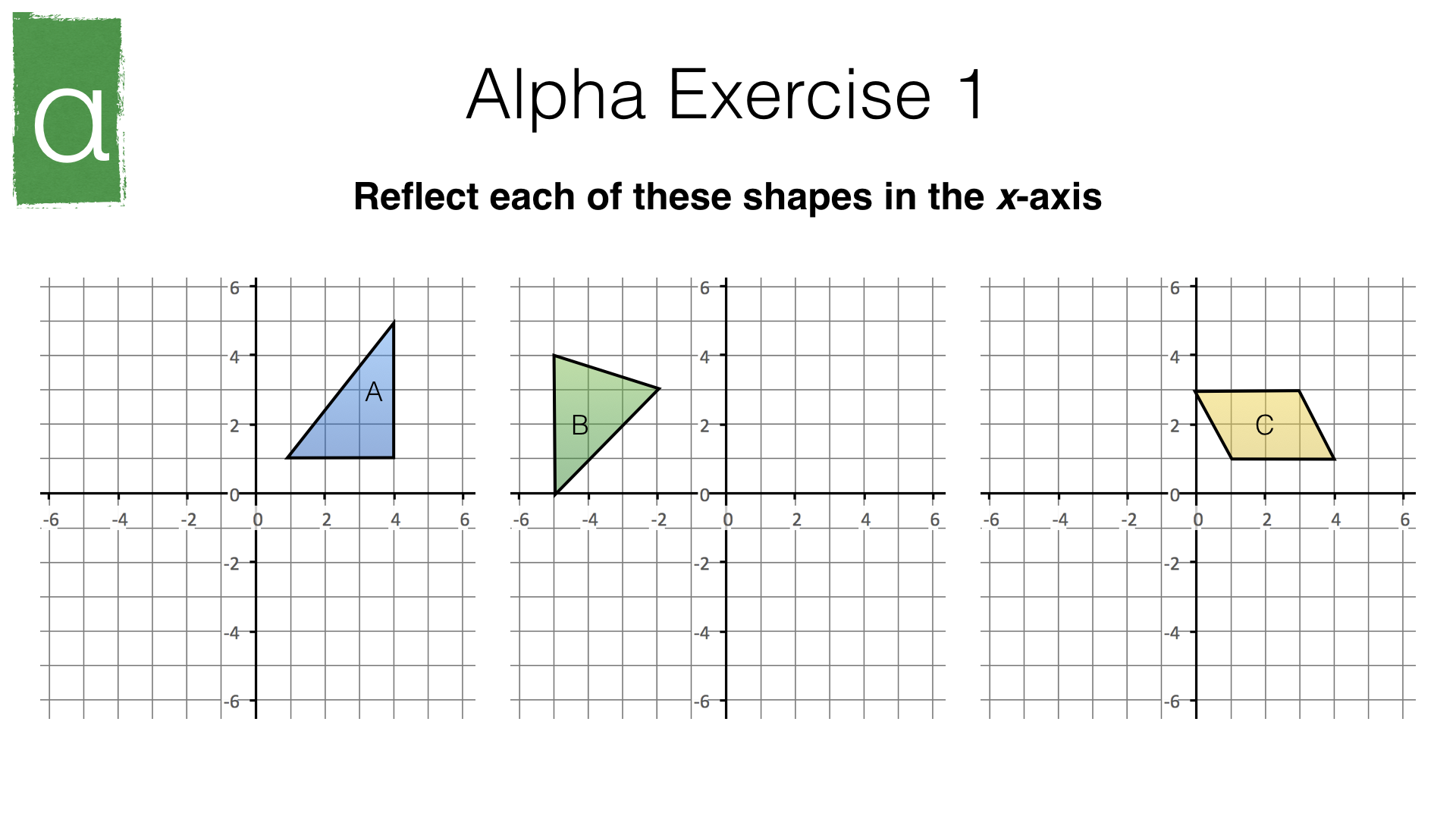
- Reflection in the x-axis or the line \(y=0\)
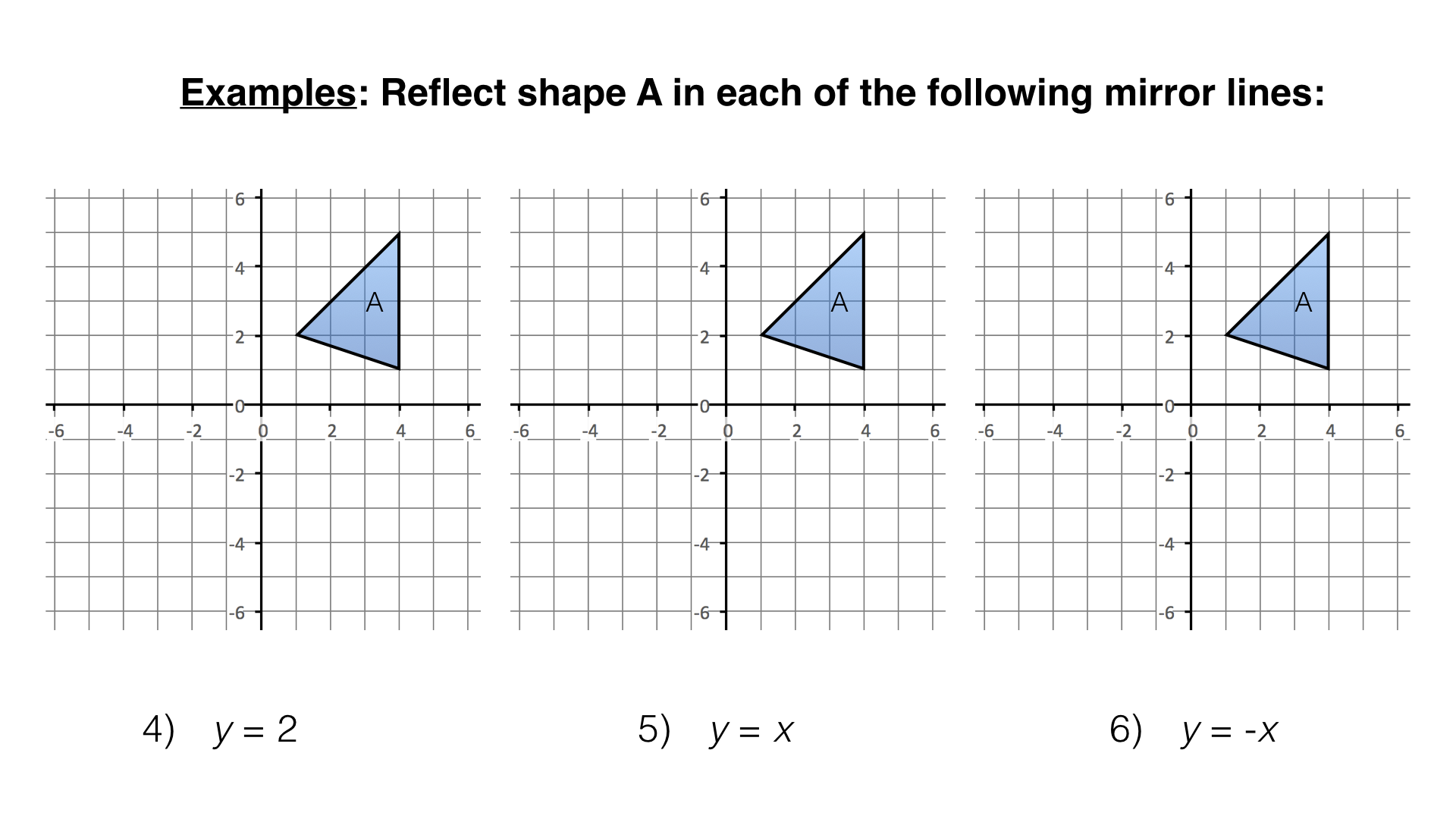
- Reflection in the line \(y=x\)
- What are the coordinates of the point to which a reflection in the line \(y=2\) maps the point with coordinates \((p,q)\)?
- \((p,2-q)\)
Teachers: log in to access these.
Reflection: Maths vs real-life
- Click reflection 1 in the applet below. You will see a correct mathematical reflection.
- Click reflection 2. You will see the line reflection replaced by a line segment i.e. a finite mirror. Mathematically, the reflection shown is incorrect. This is because we cannot find a perpendicular distance between the object and the mirror.
- Click reflection 3. Even the though the reflection shown was mathematically incorrect, it is correct from a real-life perspective, as you might have learned in science. A suitably located person will be able to see a reflection of the triangle in the finite mirror.
Reflection in a curve
Reflection in a curve does not come up at GCSE. It is nevertheless a fun thing to try, and this activity highlights an important idea about reflection and an important idea about all transformations.
Firstly, this helps draw attention to perpendicular distances. To find the perpendicular distance from a point to a circle, simply position your ruler so that it joins the point of interest to the centre of the circle.
Secondly, because of the curved mirror, it is not possible to simply pick two points to reflect and then to join them up with a straight line. Instead, you have to pick and reflect lots of points to get a good sense of what the image will look like. This helps reinforce an idea common to all transformations: when you transform an object, you transform all points on that object. (Students sometimes think that they only transform vertices. Procedurally, they may only be doing that, but this is a shortcut that leads to them transforming all points once the vertices are joined together using straight line segments. This only works because GCSE transformations always map straight lines to straight lines.)
Suggested activity
- Use the grey <> tool to move the line horizontally, keeping it to the left of the semicircle. Once you’ve decided where you’d like the line, do not move it again. Keep it fixed.
- Tick the “Show and mark reflection” box. Now slowly drag the blue point up and down the line to form the reflection.
- To focus on what’s happening, you can hide the line by unticking the “Show line box” and ticking the “Show the perpendicular” box.
Students can try this activity for themselves with just a pencil, ruler, compasses, and plain paper. Students will need to measure, to the nearest mm, distances from several points on the line to the circle, and mark the reflections of each point. As noted above, to measure distances correctly, the ruler needs to be positioned so that it joins the point on the line that’s being reflected to the centre of the circle, with the 0 at the point on the line. After marking 20-30 points, students should get an idea of what the reflection will look like.
Teachers: log in to view this content.