Enrichment sessions 7 and 8
We have added resources for Enrichment sessions 7 and 8.
Session 7, titled Lucky seven, looks at five probability problems—including the infamous Monty Hall problem.
Session 8 looks at the concept of infinity, starting with Zeno’s paradoxes and touching on infinite sums, continued fractions, nested surds, and Cantor’s arguments regarding countability of infinite sets.
TopTopics and Random Question Generators
Questions on surds have been added to TopTopics:
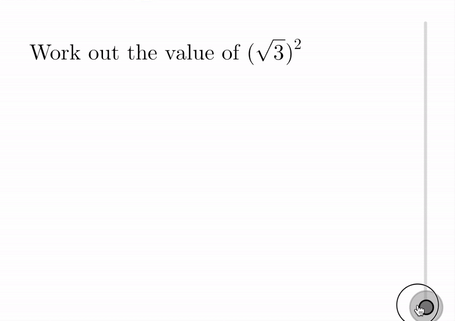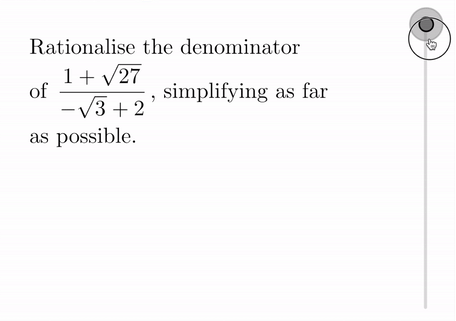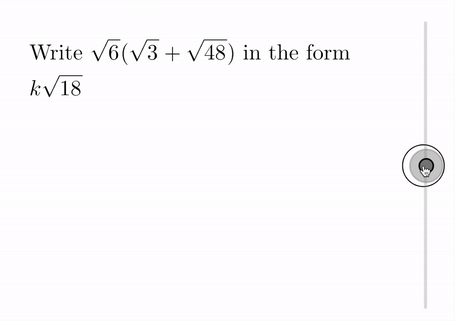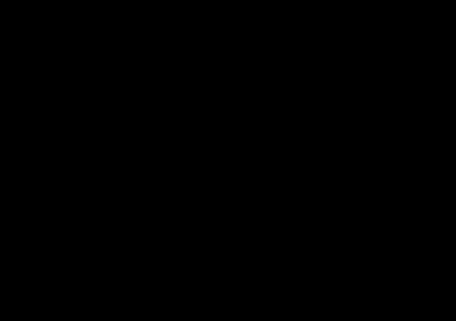
Additionally, we have included three sets of quick-access random question generators under the Teacher Resources for topic N8b on surds. The first set is made up of questions such as the following:
- The first set includes questions such as \(\text{Simplify } \sqrt{98}\) and \(\text{Simplify } \sqrt{5\frac{1}{16}}\).
- The second set includes questions such as \(\text{Simplify } \sqrt{7} + \sqrt{63} \) and \(\text{Simplify } \sqrt{54} \times \sqrt{24}\).
- The third set includes questions such as \(\text{Write } 5\sqrt{7} \text{ as the square root of a single number}\) and \(\text{Write } \sqrt{7} \left(\sqrt{45} + \sqrt{20}\right) \text{ in the form } k \sqrt{35}\).
Geoboard activities
We have added geoboard activities for a couple of topics, including this one for G20a Pythagaras’ Theorem:
When you create a square whose area is one of those stated, the applet indicates that you have been successful.
Double-sided counters and algebra discs – groupable and with one-click turning over of groups
Double-sided counters are a great way to introduce the concept of zero pairs to students before getting them working with directed numbers. The applets we have created here allow you to group together counters or discs and then turn them all over with one click. This is particularly useful when it comes to subtraction with negative numbers: we can introduce students to the idea that subtracting a quantity is simply the same as adding its additive inverse. So \(5 – (-2) = 5 + 2 = 7\), as shown: