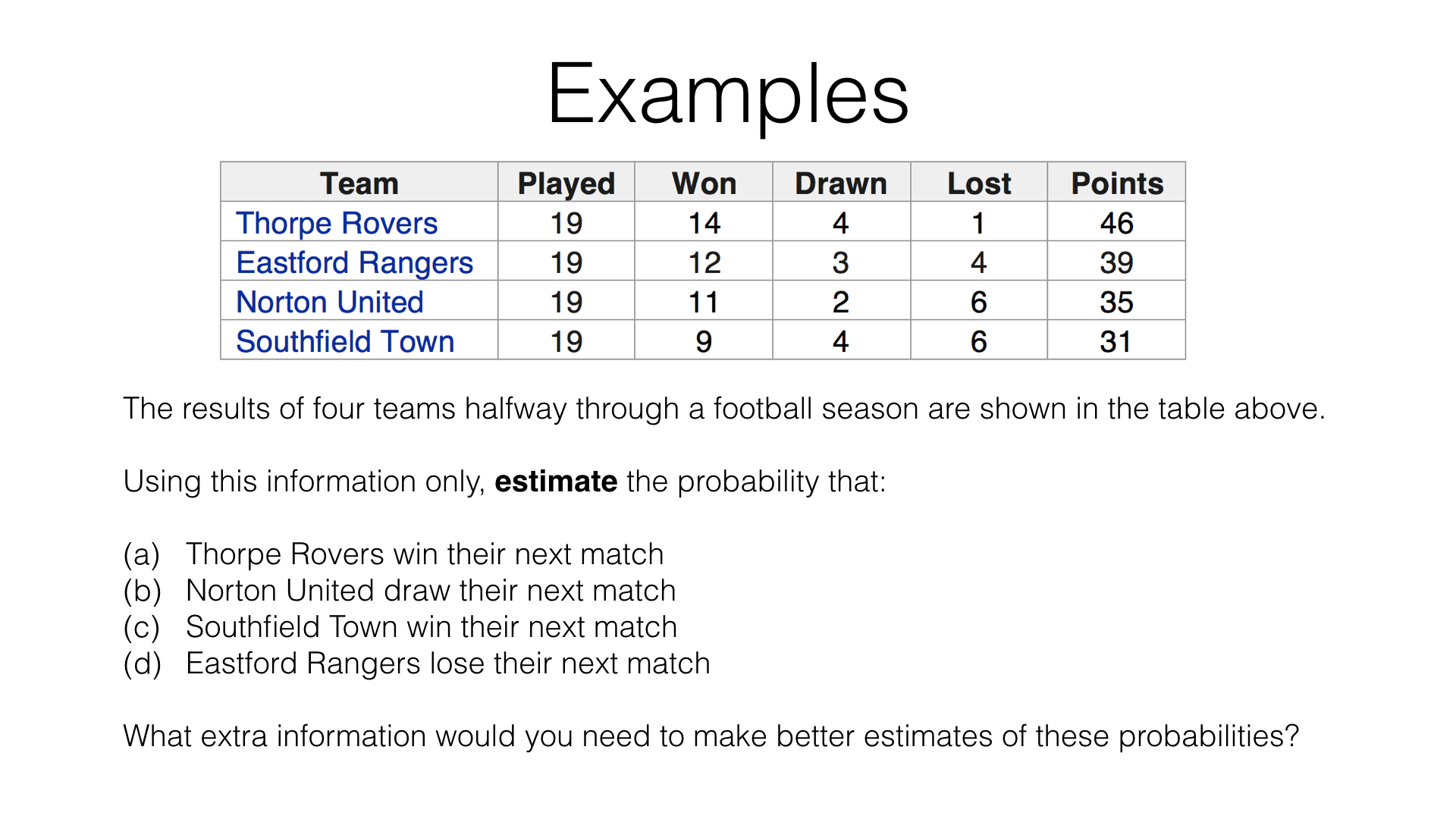
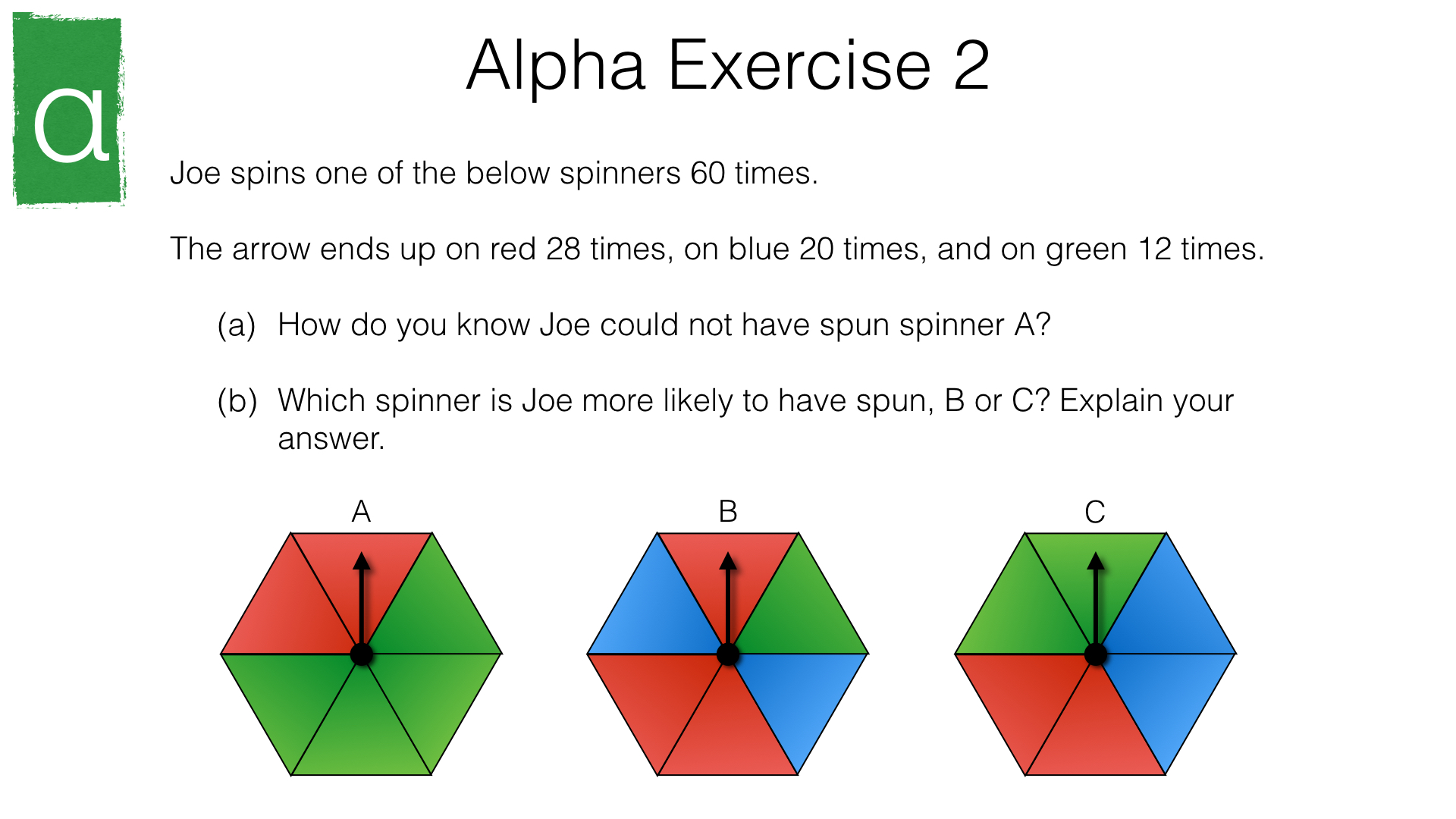
This is the students’ version of the page. Log in above for the teachers’ version.
Prerequisites
Relative frequency (experimental probability)
Click the tabs for extension tasks…
Callum flips a coin several times. The coin comes up heads 36 times. Callum worked out that the relative frequency of the coin coming up heads is \(\dfrac{9}{17}\). How many times did he flip the coin?
Hover for answer:
68 times, since \(\dfrac{9}{17}=\dfrac{36}{68}\)Jamie flips a coin several times. The coin comes up tails 40 times. He then works out that the relative frequency of the coin coming up tails is \(\dfrac{11}{25}\). Could Jamie be correct? If so, how many times did the coin come up heads? If he has made a mistake, explain how you know.
Hover for answer: Jamie is wrong. \(\dfrac{11}{25}\) cannot be written as \(\dfrac{40}{n}\) where \(n\) is an integer.
Teacher resources
Links to past exam questions
Teachers: log in to access these.
In the real world
Teachers: log in to view this content.