At MathsConf 25, I spoke very briefly about trigonometry, amongst other things—such as pantographs, nomograms, and slide rules. Here I’ll share some of my thoughts on teaching trigonometry, which I’d been pondering for a while.
What I found unhelpful
In the past, I’ve often used applets like this one:
A problem is that there’s a lot happening here. I thought that I was perhaps using the applet too quickly for all students to really take in, but manually controlling the animation (together with extra narration) didn’t help me “get” all students on board. The deeper problem isn’t that there’s a lot happening in the above animation. The real issue has been that not all students were ready to take it all in when they encountered this concept. A possible solution might involve planting seeds months or even years beforehand, to help get them to a position where they’re not overwhelmed by the above idea.
Calculators, disembodiment, and trig tables
While at heart I am a nonagenarian (albeit in a thirty-something’s skin), I am in fact young enough to have had my own scientific calculator throughout my school years. This means I was never exposed to trig tables at school. Even as a teacher, for years, I never thought to talk about trig tables when teaching trigonometry. The closest thing that my students would have seen would have been a table showing exact trig values for special angles:
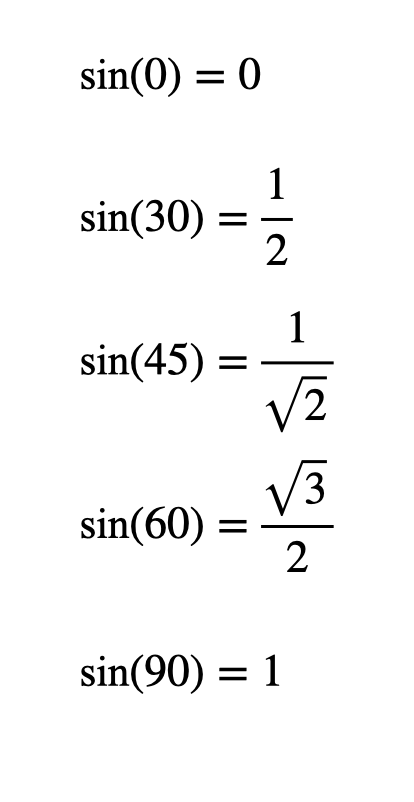
I think it is a great shame that so many of my students never got to see proper trig tables. Consider this problem. You’ll get to a stage where you want to work out \(\text{sin}(35)\).
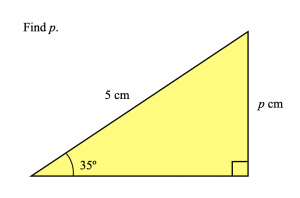
You can of course tap \(\text{sin}(35)\) into a calculator to find it is about 0.574, but that’s pretty much all you find out. You get a “disembodied” value that appears as if by magic. If you had to look up \(\text{sin}(35)\) in a trigonometric table, however, it would feel a lot less magical—and (eventually) more understandable. There are three things I like about trig tables:
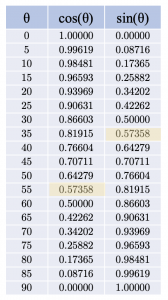
- Looking things up in a table this way reinforces the idea that trig functions are functions. Occasionally I’ve found students that seem to think \(\text{sin}(35)\) is \(\text{sin} \times 35\). I’m not sure they’ve necessarily developed their thoughts as far as formally seeing \(\text{sin}\) as a constant like \(\pi\), but they’ve certainly not fully grasped that it’s a function. They may even cancel in ways consistent with this misconception eg \(\dfrac{\text{sin}(60)}{10} = \text{sin}(6)\).
- A trig table gives you a sense of where trig functions are increasing and decreasing. While looking for the relevant entry eg \(\text{sin}(35)\), you can’t help but scan other parts of the table. We can see that the sine of an angle is clearly increasing as an acute angle approaches a right angle, and that the opposite is true for the cosine.
- Thirdly, and relatedly, you get a sense of the symmetries involved. Of course, it is important for students to understand trig graphs, but appreciating graphs can sometimes be harder than appreciating tables of values. I would suggest that students will more readily spot that \(\text{sin}(x) = \text{cos}(90-x)\) from this table than from the graphs. They might not make this algebraic leap for themselves, but they are likely to spot how the sine and cosine columns for angles from 0º to 90º are the same, but in the opposite order. From here, it feels natural to investigate why this might be, perhaps by thinking about right-angled triangles.
Of course, I’m not arguing that we should ditch calculators. I am suggesting that there might be value in using trig tables first, and only then showing students how they can use their calculators.
In a future post, I’ll share some more general thoughts about planting mathematical seeds. Here I’ll limit myself to ideas based on the unit circle. In particular, here are some activities that are all based on a single GeoGebra applet that I shared in my MathsConf workshop. The idea is that these students can access these activities at various stages before they formally have to start using trigonometric functions.
Coordinates and symmetry
Here is an activity that students can access long before they formally meet trig functions. It’s surely too much for an introductory unit on coordinates, but it might be appropriate if you’re revisiting coordinates with confident students, or perhaps if you’re looking at rotational and reflection symmetry. There is no need to mention the phrase unit circle at all here.
Properties of triangles
Here is an activity that would fit into a unit where students are looking at properties of triangles. Technically, the circle here need not be the unit circle; it could have any radius. This activity isn’t so much intended as an investment that will pay dividends when students encounter trig, but rather when they encounter circle theorems. It also offers a potential way to get them thinking about modular arithmetic (or clock arithmetic)—I think it’s a shame that this isn’t more of a thing in schools:
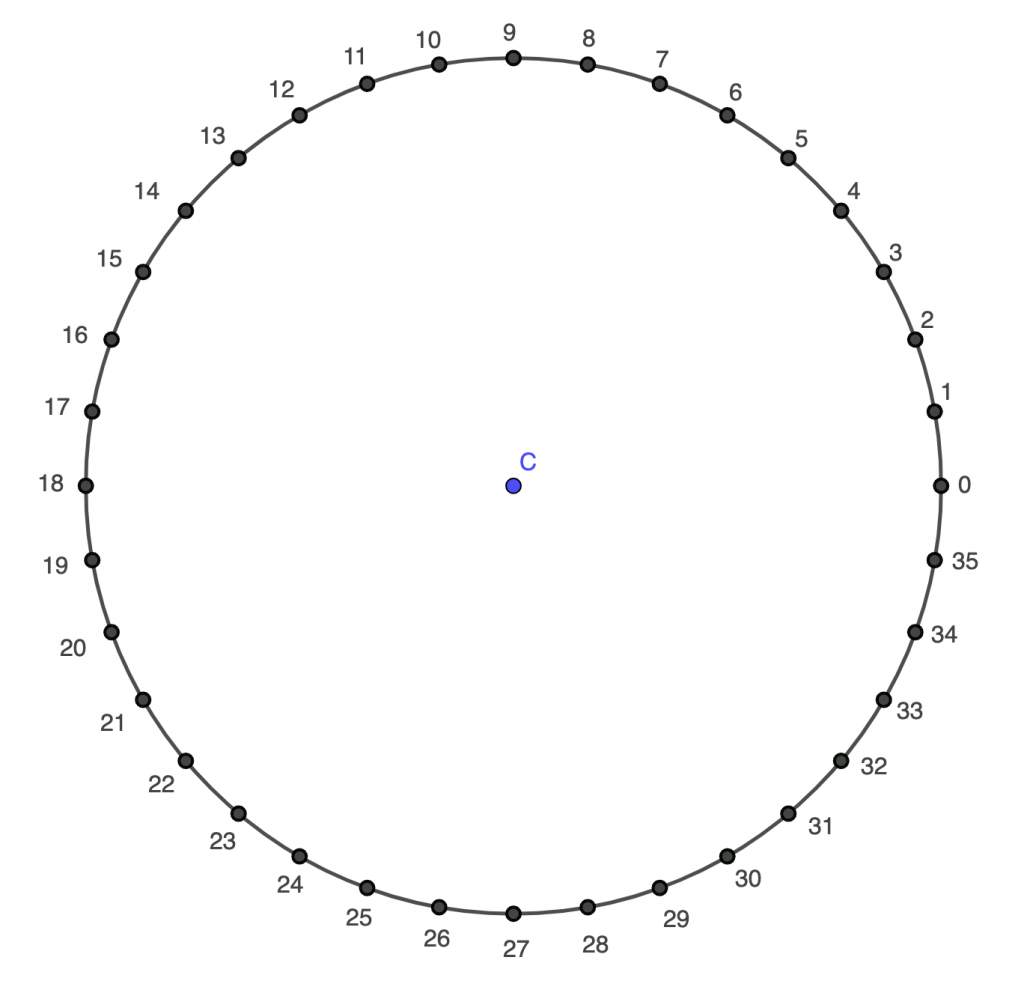
- Write down the labels of 3 points on the circumference that you can join to form an equilateral triangle. How many different sets of 3 points can you find?
- You are now allowed to use the point C. Write down the labels of 3 points that you can join to form an equilateral triangle that is not congruent to those you found in question 1.
- Write down the labels of 2 points that, together with C, form an isosceles triangle. Can you form more congruent isosceles triangles using different sets of three points? How many different sets of points can you find?
- Write down the labels of 3 points that form an isosceles triangle that is not congruent to the ones you found in question 3.
- Write down the labels of 2 points that, together with C, do not form an isosceles triangle (or even an equilateral triangle). How many different sets of points can you find?
Functions
As mentioned above, I’ve often shown students how the sine and cosine graphs can be generated from an animation on the unit circle, and found there are often some for whom nothing “clicks” when they see it. I have found that students get a more visceral appreciation of what’s happening if they complete an activity like this. Students can click on the point in the applet below to (painstakingly!) populate the table for themselves. Here, \(\text{f}(x)\) is \(\text{cos}(x)\) and \(\text{g}(x)\) is \(\text{sin}(x)\), but I’ve chosen not to include the names of the trig functions at this stage. That’s so they can be revealed at the end, with a bit of fanfare. “You’ve probably seen those \(\text{sin}\) and \(\text{cos}\) buttons on your calculator. Well,..”
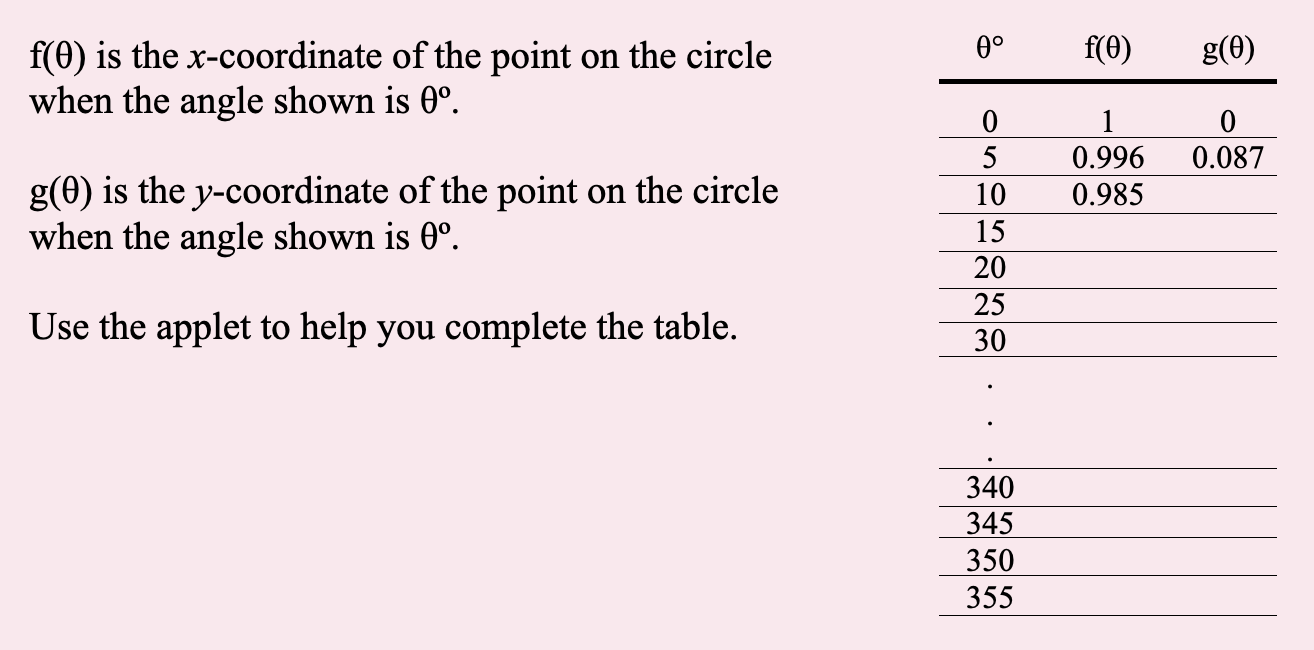
This may seem tedious, but there are three points I’d make in response to that. The first is that the tediousness is part of what helps gives a more visceral appreciation of the trig functions—and their graphs, if they go as far as hand-plotting them using their populated tables. Secondly, this task needn’t be as tedious as it seems—we can reuse the idea from above and encourage students to spot rotational and reflective symmetries. If they know that the point at 5º has coordinates \((0.996,0.087)\), then they should immediately be able to write down the coordinates for seven other points—the ones at 85º, 95º, 175º, 195º, 265º, 275º, and 355º. Thirdly, if it still seems a bit much, the applet and table can be adapted so that students are only populating the table for, say, multiples of 10º rather than multiples of 5º.
I wouldn’t include this anywhere near an introductory lesson on functions. I tend to use it much later, alongside examples of other “exotic” functions—by which I mean functions that don’t merely apply the four operations and exponentiation to an input to generate an output. I mentioned above that students sometimes don’t appreciate that trig functions are functions for various reasons. Another contributing factor might be that they’ve only encountered simple, “non-exotic” functions before. Exposure to a broader variety of functions, years before they formally encounter trig functions, might help them accept sine and cosine as “legit” functions (to use their vernacular).
Gradient
In the above activity, I only focussed on sine and cosine (though I would, for the most part, keep the names hidden from students). But we can plant some \(\text{tan}\) seeds while looking at gradient. Again, this wouldn’t make sense in an introductory unit on gradient. But at some point after students are introduced to functions and to gradients, they could complete the following activity using a version of the previous applet (updated to show more decimal places, to allow more accurate calculation of the gradient):
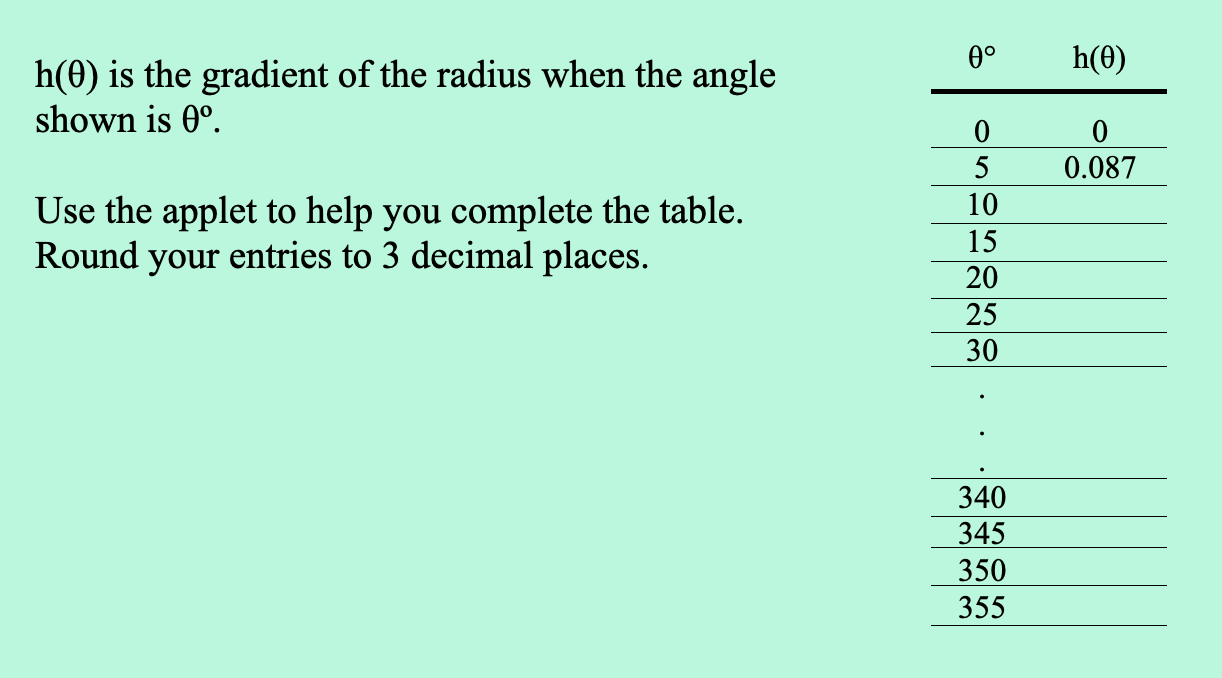
There is considerable overlap between this and the above activity, but I think I prefer to keep this one separate for two reasons. Firstly, it provides yet another spaced opportunity for students to encounter the unit circle. Secondly, it allows students to focus on the key ideas here—eg that angles 180º apart gives us line segments with the same gradient.
Similar triangles
Having looked at similar triangles and used the unit circle, students can fill in the blanks here before being taught the usual procedures for right-angled triangle trigonometry. They don’t even need to know the definitions of opposite and adjacent at this stage.
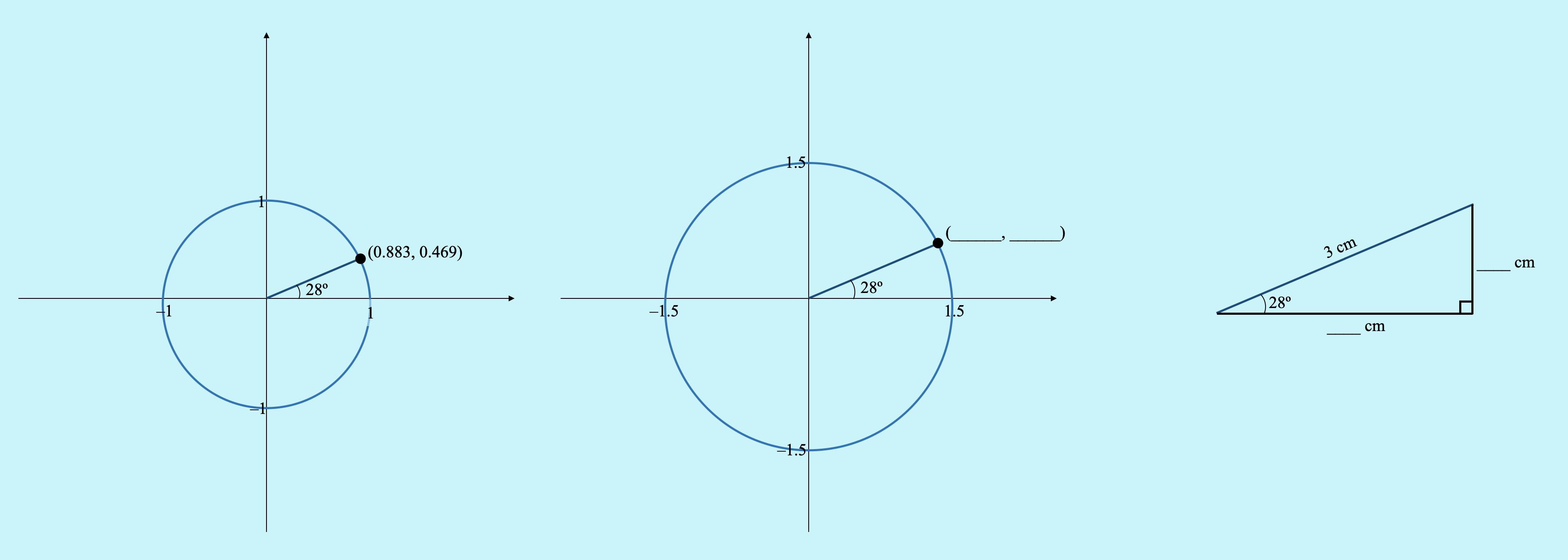
Final thoughts
This post is now quite long, so I’ll just add that what I like about these activities are the interesting digression opportunities that present themselves. These digressions may not be totally relevant to trigonometry, but can be fantastically mathematical in their own right. I mentioned modular arithmetic above—there’s lots of potential there to explore aspects of regular polygons, including interior and exterior angles. From there, it’s possible to make a little hop to “polygons” with non-integer numbers of sides. For example, on a version of the applet with 36 points on the circumference, try joining every 8th point until you get back to your starting point. In what ways is it reasonable to call this a 4.5 sided polygon?