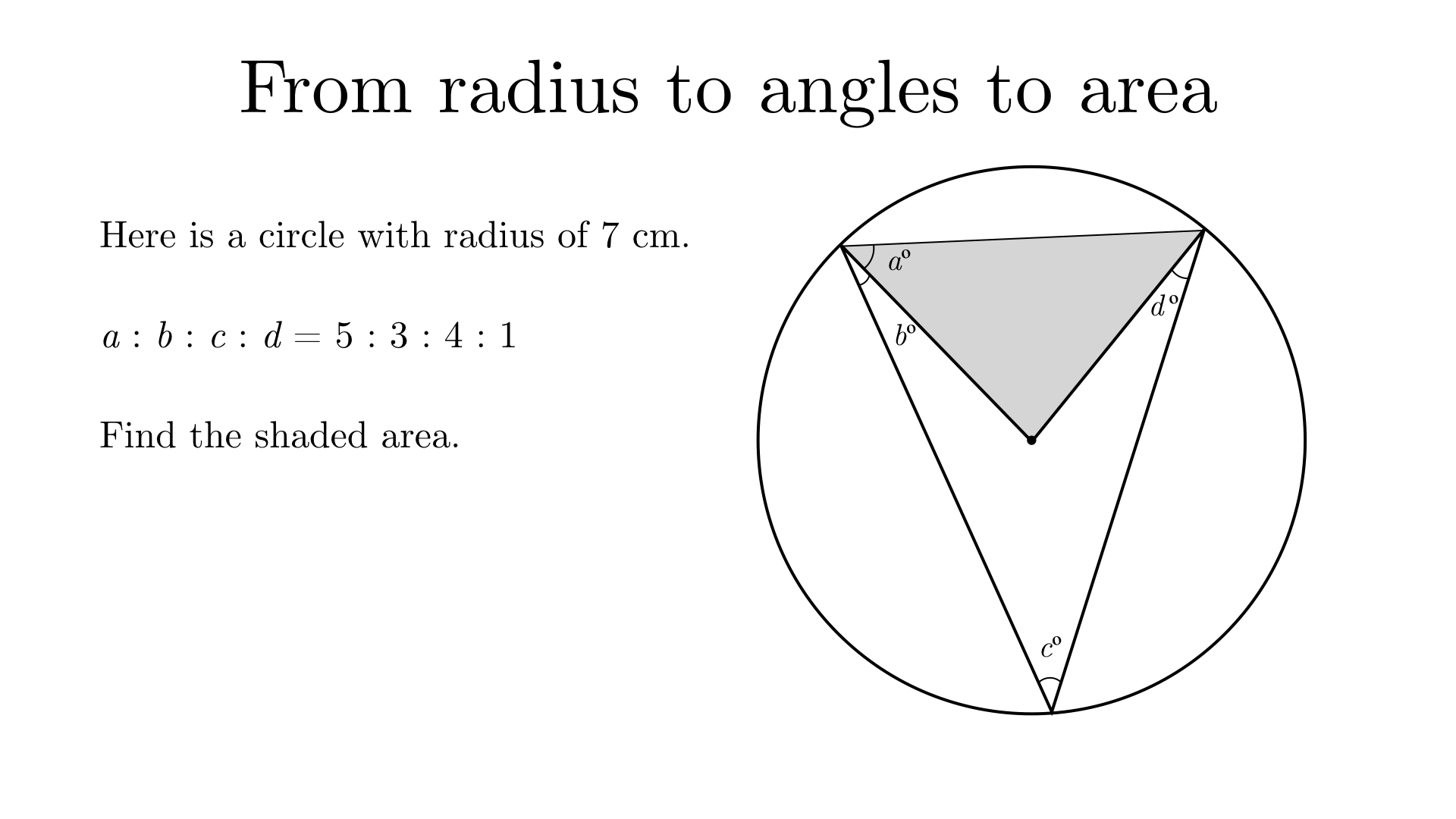
The shaded triangle is isosceles as two of its sides are radii. Therefore, it has another angle of \(a\)º.
Consider the triangle with the 3 points on the circumference that has interior angles of \((a+b)\)º, \(c\)º, and \((a+d)\)º. These must sum to 180º so \(2a+b+c+d=180\).
From the given ratio, we can say that \(2a:b:c:d = 10:3:4:1\). Given that \(2a+b+c+d=180\), we can share 180 in the ratio \(10:3:4:1\) to find that \(2a = 100, b=30, c=40, d=10\). Therefore, \(a = 50, b=30, c=40, d=10\).
The angle at the centre of the circle in the shaded triangle is equal to double the angle \(c\) at the circumeference, so is \(80\)º.
The area of the shaded triangle is \(\frac{1}{2}(7 \times 7)\text{sin}(80) = 24.1 \text{ cm}^{2}\) to 3 significant figures.