This post outlines how a worksheet mix-up changed how I introduce the use of protractors to classes I suspect will struggle with this topic. In this blog post, protractor refers to standard half-circle protractors that have inner and outer scales.
One of my earliest disastrous lessons occurred early in my first year of teaching, back in 2008. I was attempting to teach bottom-set Year 7 how to measure angles, and I made the rookie error of giving out protractors straight away. While some of the students were at least able to perform the task of measuring non-reflex angles by the end of the lesson, most could not even correctly position protractors. I remember scrambling around the room, attempting to give individuals one-to-one guidance where needed, but actually having to deal with poor behaviour arising from the inappropriateness of the sequencing of tasks.
An improvement that still left a lot to be desired
For a long time subsequently, my lessons on measuring angles typically consisted of three worksheets, each with a series of similar questions:
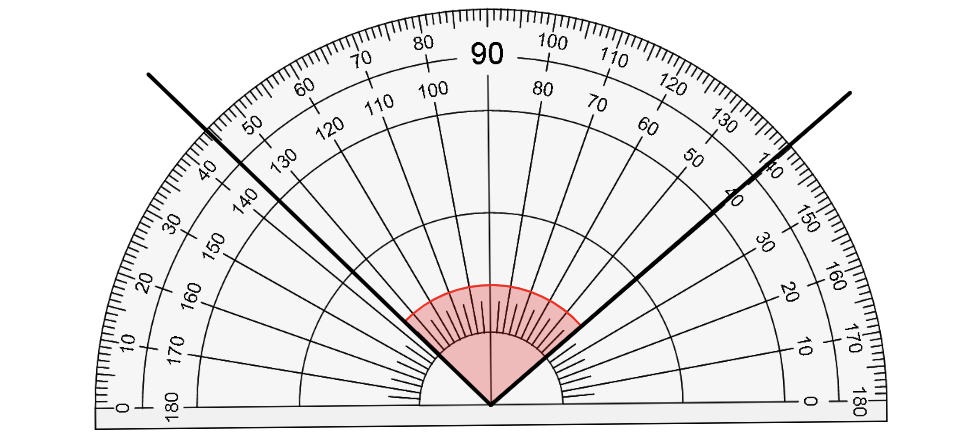
Worksheet 1 consisted of questions such as the one immediately below, where a protractor was printed on the angle, correctly positioned. As such, students could focus on simply reading the protractor without having to worry about physically positioning a real protractor:
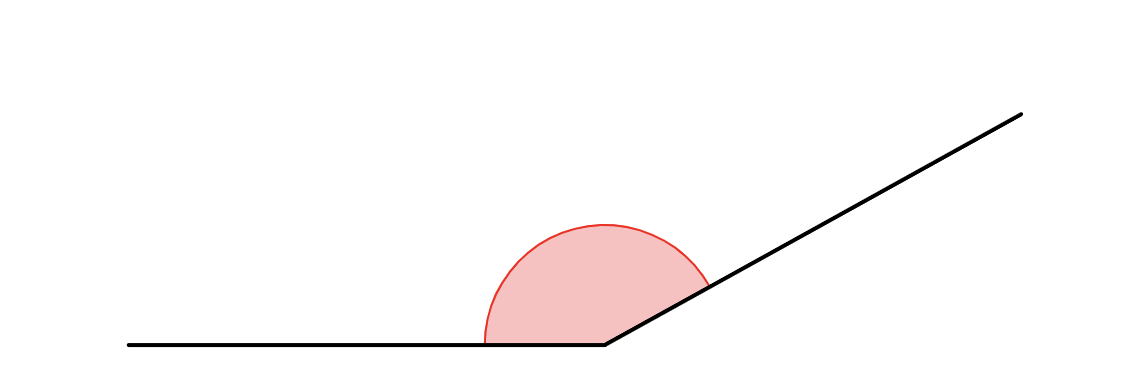
Worksheet 2 consisted of a some angles drawn on the page, such as the one below. Only at this point students would have to use real protractors:
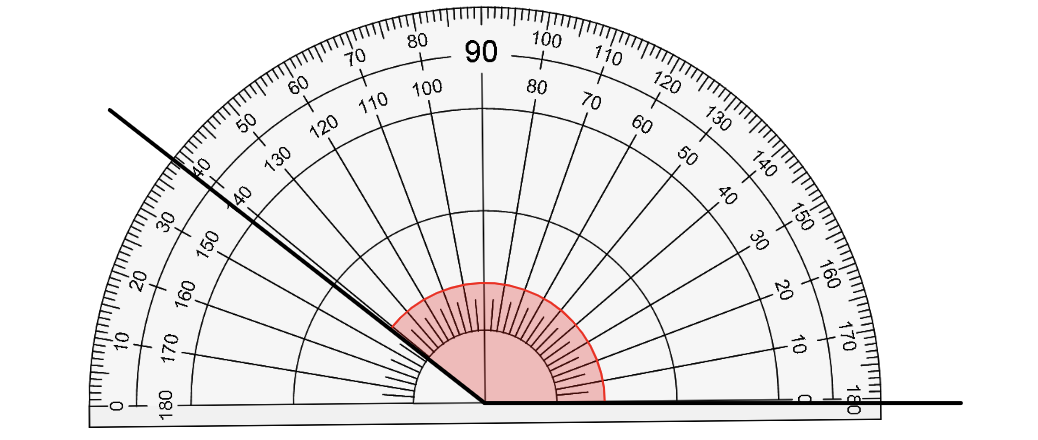
Worksheet 3 consisted of what I then considered “extension” problems such as that pictured below. Here, students would have to work out the correct angles based on the “incorrectly” positioned protractor printed on top of the angles:
This approach was significantly better than that I used in my disastrous, first lesson on the topic. Nevertheless, it was still rarely satisfactory. There would always be at least one student that struggled—either when positioning their protractor “correctly” or when deciding whether to use the inner or outer scale of the protractor.
The lucky mix-up
A few years ago, I accidentally handed out Worksheet 3 to students instead of handing out Worksheet 1 at the start of one lesson. Rather than attempt to rectify the mistake, I went along with it. I explained the definitions of vertices and rays, as usual. I told students to notice that the centre point of the protractor’s base was positioned on the vertex. Finally, I told them how to work out the angle by finding the difference between the numbers corresponding to the protractor markings intersected by the two rays. I noted that it did not matter whether you used the inner or outer scale, but that you had to be consistent.
This turned out to be quite a liberating experience. When I handed out Worksheet 2 and got students using real protractors, they did not have to worry about positioning their protractors in the “correct” way i.e. with one of the rays aligned with 0º on the protractor. They
- simply had to ensure that the centre of the protractor was placed on the vertex (and that the protractor was on top of the two rays, but they seemed to manage this instinctively with no guidance, even when rays pointed “downwards” on their pages);
- then did not have to decide between the inner or outer scale, but could pick either one; and finally
- had to find the difference between the readings corresponding to the two rays.
While this third step constituted an extra bit of work compared to positioning a protractor in the “correct” way, subtraction was a relatively basic skill compared to the amount of decision-making required when attempting to measure angles the “correct” way. What was especially delightful, however, was that most students deduced for themselves that they could deliberately choose to rotate the protractor so that one of the rays was aligned with 0º on the protractor, thus making the final step easy/redundant!
While I have always leant towards explicit instruction for the most part (primarily because behaviour is easier to manage rather than because I’ve always known about its efficacy), this case illustrates one benefit of not being explicit, which may be an advantage worth exploiting in certain situations. The advantage was that I, as the teacher, could quickly see that certain students had reached a particular level of understanding—because they had deduced for themselves that aligning a ray with 0º was an efficient thing to do. If I had “just told them” to do this, they might well have performed the instruction, but the extent to which they really understood why they were following the instruction would not have been as immediately evident.
Summary
Based on how well that lesson went, I deliberately began to introduce this topic using problems such as those on Worksheet 3. The two main advantages are firstly that students only need to focus on positioning the centre of the protractor’s base (and needn’t worry about lining up a ray with a 0º marking) and secondly that they can avoid having to decide whether they need to use the inner or outer scale of the protractor. Since using this approach, I have found that students enjoy greater success getting to grips with using protractors than they did when I tried to teach them to position protractors “correctly” from the outset. I think it also helps embed the idea of angles as a measure of “difference” in turn between two rays.
Having said that all this, I don’t consider myself a particular specialist with low-ability KS3 students (KS5 is more my up my street), so there may well be some better strategies out there.